Affine Geometrie / Affinitäten 11.2022

0. Vorbemerkungen

Abschnitt überspringen

Dieser Text bietet eine Einführung in die geometrischen Affinitäten, einmal unter dem anschaulichen Blickwinkel der Darstellenden Geometrie, zum andern unter dem strengeren Bickwinkel der Analytischen Geometrie.

Wie anschaulich man mit dynamischer Geometrie eine strenge math. Theorie erschließen kann, wird im Folgenden mit Hilfe des Programms EUKLID DynaGeo von Roland Mechling gezeigt. Dazu wird in diesem Text der DynaGeoJ-Viewer von R. Mechling verwendet. Alle Konstruktionen sind im Haupttext nur verkleinert dargestellt. Durch Anklicken gelangen Sie zu den zugehörigen DynaGeo-Fenstern in sinnvoller Größe.

Aktueller Hinweis:
Die dynamischen Inhalte sind mittlerweile nicht mehr direkt aufrufbar, weil alle etablierten Browserhersteller die Programmiersprache Java nicht mehr unterstützen. Siehe weitere Details in Tipps zum DynaGeoJava-Viewer.

Um Punkte in einem DynaGeo-Fenster zu bewegen, müssen Sie den Mauszeiger an einen der gekennzeichneten Punkte der Konstruktion schieben, bis der Mauszeiger sich in ein Zangensymbol verwandelt und dann den Punkt mit gedrückter Maustaste verschieben. Sie schnappen also einzelne Punkte mit der Zange und verschieben sie dann. Wenn Sie so eine Konstruktion zu sehr durcheinander gebracht haben und daher zur Ausgangskonstruktion zurückkehren wollen, laden Sie die ganze Unterseite im Browser nach (oder kürzer: rechtsklicken Sie in eine leere Stelle des aktuellen DynaGeo-Fensters und wählen Sie dann im Kontextmenü Zeichnung neu laden).

Wir sparen uns also aufwändige Berechnungen (obwohl die dazu nötige Theorie im Folgenden knapp dargelegt wird und vor allem über die Linkliste im letzten Abschnitt erreichbar ist) und setzen auf die Konstuktionskunst von DynaGeo, die uns zum Experimentieren und damit zum spielerischen Entdecken verleiten soll.

Dabei soll nicht vergessen werden, darauf hinzuweisen, dass spielerisches Entdecken keinen mathematisch (nötigen) Beweis ersetzen kann, aber sehr wohl eine mathematische Vermutung zu widerlegen in der Lage ist, falls diese falsch sein sollte!

1. Einführung: Bauanleitungen

Abschnitt überspringen

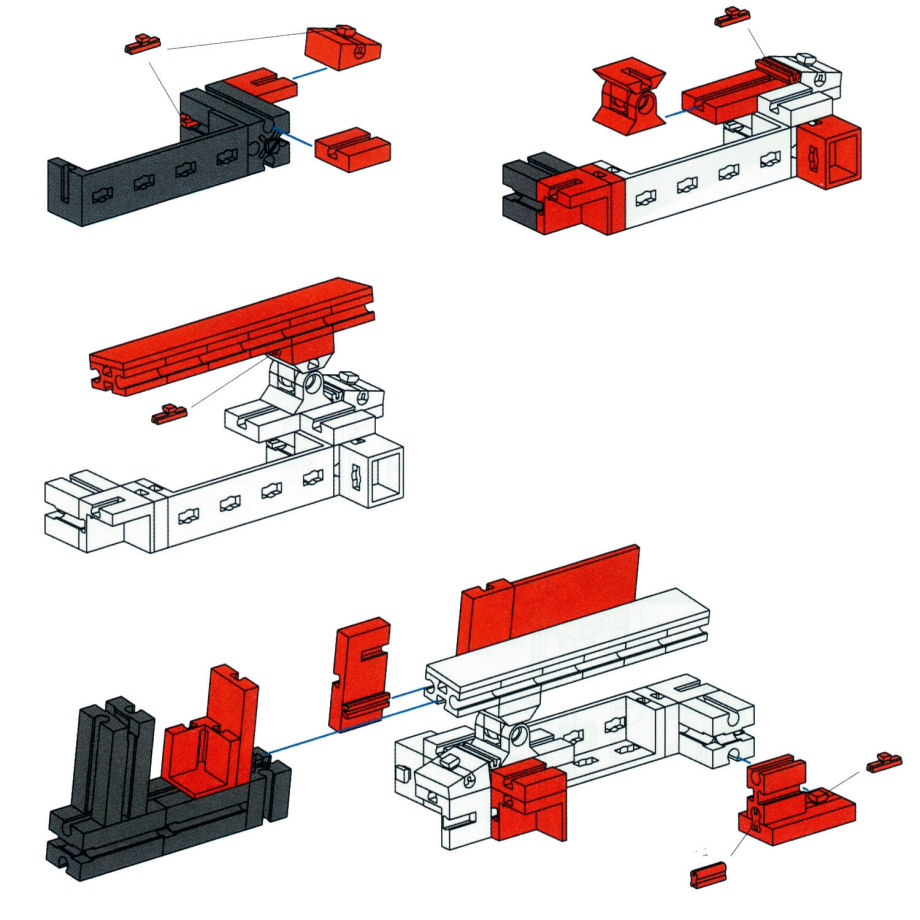
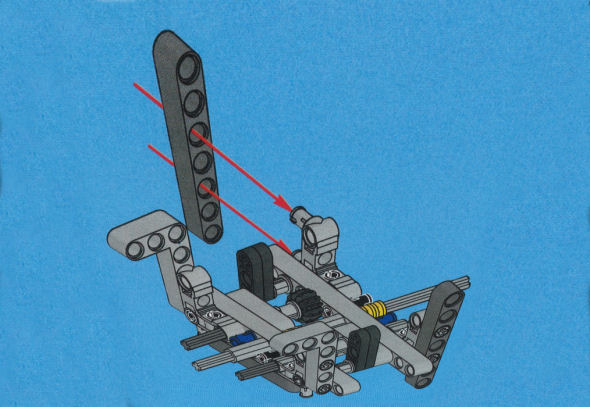
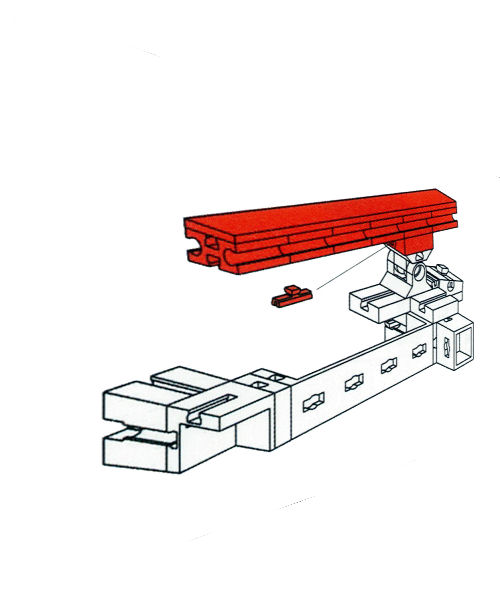
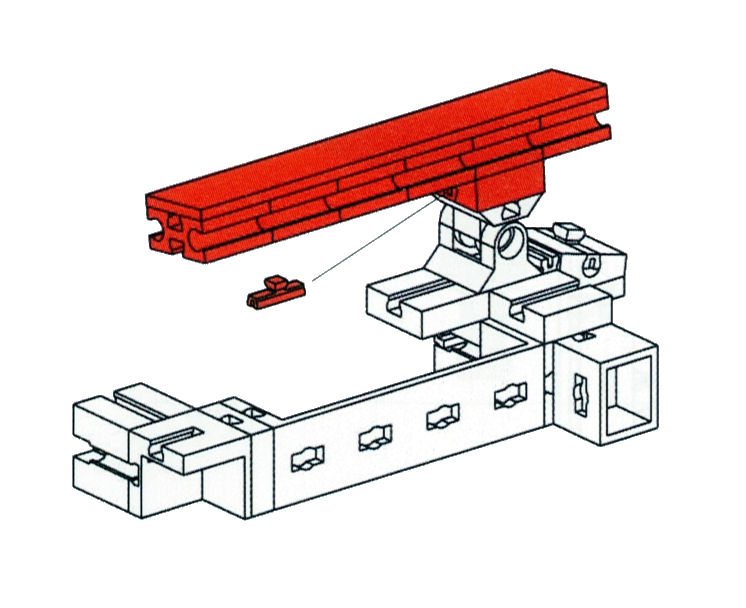
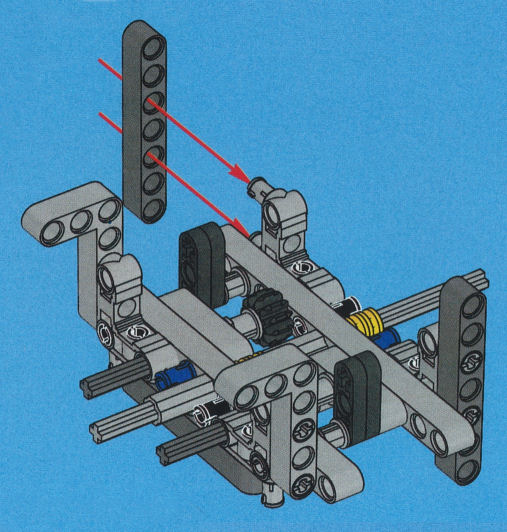
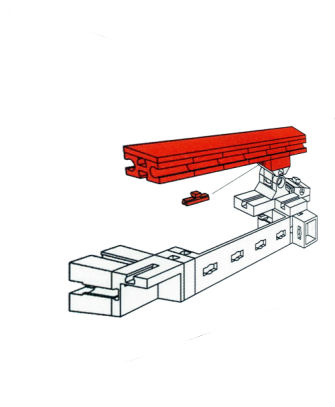
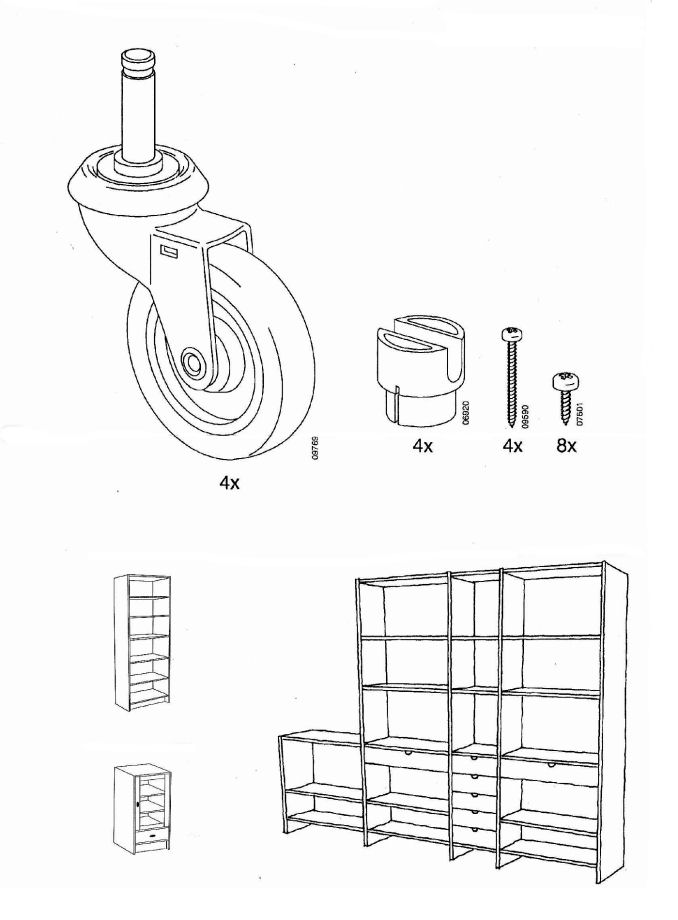
Die folgenden Bilder sind Fotomontagen von Baugruppen, die diversen Bauanleitungen entnommen worden waren. In Bild 1.1 ist eine Baugruppe aus der Fischer-Technik-Profi-Bauanleitung Dynamic abgebildet. Bild 1.2 zeigt eine Baugruppe aus der Lego-Technik-Bauanleitung Mobiler Schwerlastkran und Bild 1.3 ist eine Zusammenstellung aus mehreren IKEA-Montageanleitungen.

Bild 1.1 - 1.3

Es ist zu vermuten, dass Kinder ab ca. 10 Jahren sicher mit den Anleitungen für technisches Spielzeug umgehen können, nötigenfalls mittels "Versuch und Irrtum". Bei den IKEA-Montageanleitungen sollte der Kunde möglichst nicht nach der Methode "Versuch und Irrtum" vorgehen müssen. Aufgabe aller dieser Darstellungen ist es, die räumlichen Baugruppen so aufs ebene Papier abzubilden, dass die räumlichen Zusammenhänge der Komponenten nachvollziehbar sind. Welche Abbildungstechnik ist dazu nötig? Gibt es günstigere und ungünstigere Abbildungsmethoden?

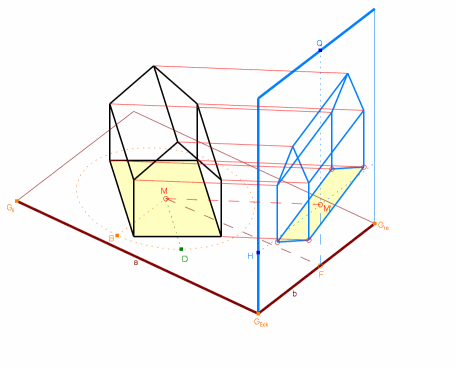
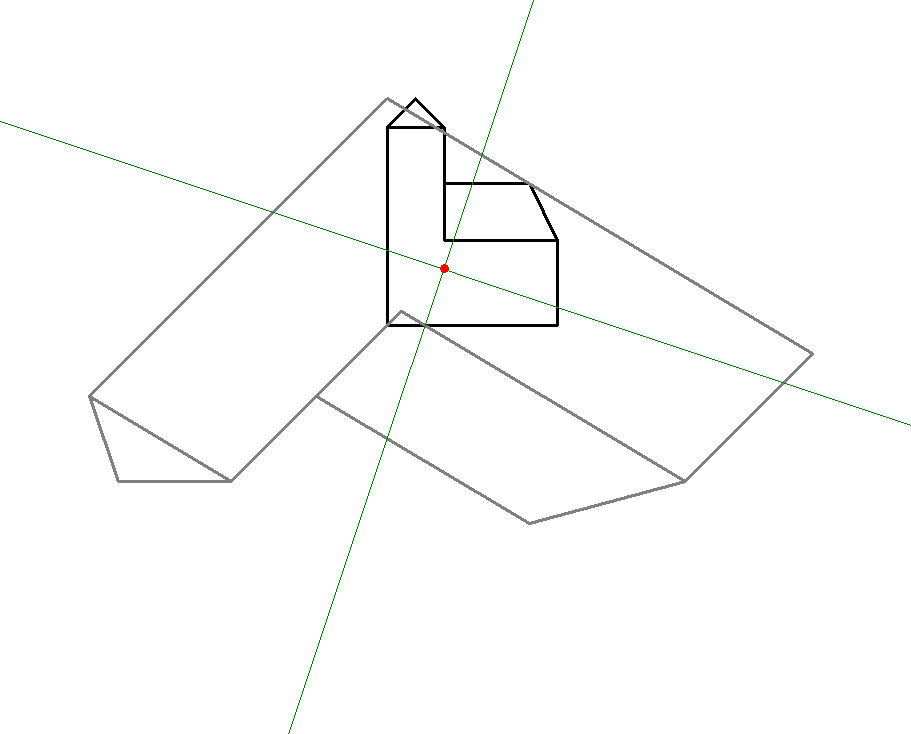
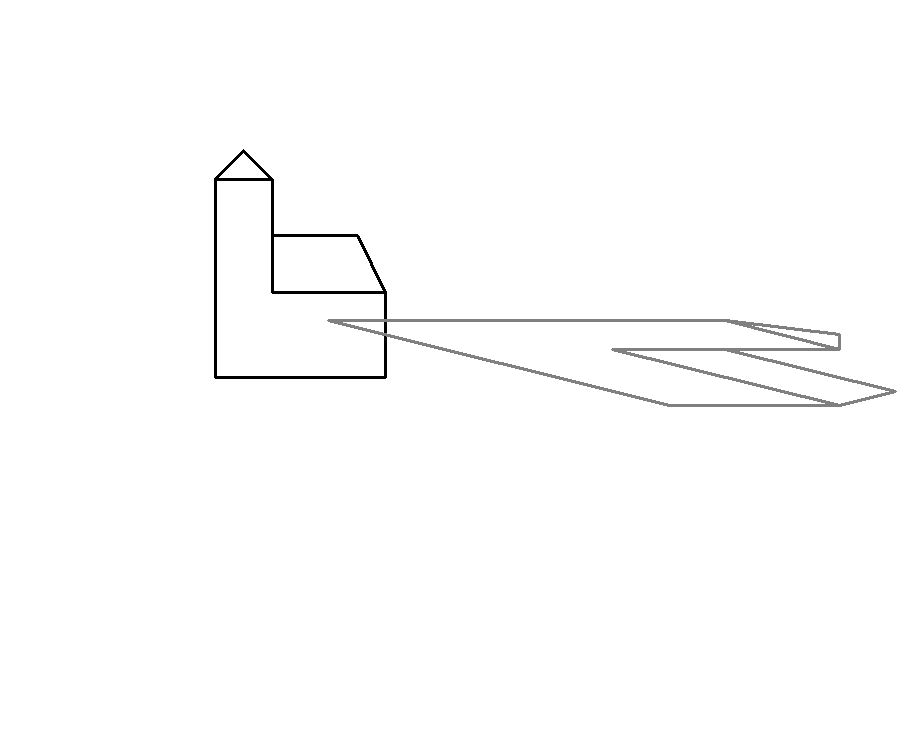
Bild 1.6 ist ein unveränderter Ausschnitt aus der IKEA-Montage (Bild 1.3), lediglich ergänzt um die "Fluchtlinien", mit deren Hilfe man zwischen Parallelprojektion und Zentralprojektion unterscheiden kann. Die braunen Fluchtlinien liefern einen "Fluchtpunkt" im Bild, die beiden blauen einen außerhalb des Bildes; beides ist typisch für Zentralprojektion (siehe Text Zentralprojektion / Perspektive). Die violetten Linien sind parallel, was auf Parallelprojektion (dieser Text) hindeutet. Wahrscheinlich haben die Entwickler der Aufbauanleitungen beschlossen, bei großen Möbeln (auch) mit Zentralprojektion zu arbeiten; schließlich sieht man in Realität raumhohe Möbel von "innen", d.h. untere Böden von oben und obere von unten. Aber nun erscheinen die Maße verzerrt: je weiter links die Seitenwangen des großen Regals angeordnet sind, desto kürzer sind sie dargestellt! Kleinere Möbel sieht man normalerweise von oben, da genügt die Parallelprojektion. Und nun stimmen die Maß-Relationen wieder.

Dementsprechend sind die Fischer-Technik- und die Lego-Technik-Bauanleitungen in Parallelprojektion ausgeführt. Die dargestellten Baugruppen sind recht klein und filigran, sie werden daher immer von oben gesehen. Da "reicht" die Parallelprojektion völlig aus. Außerdem bleiben so die Abmessungen (relativ) unverzerrt. D.h., z.B. die Lochabstände bleiben konstant.

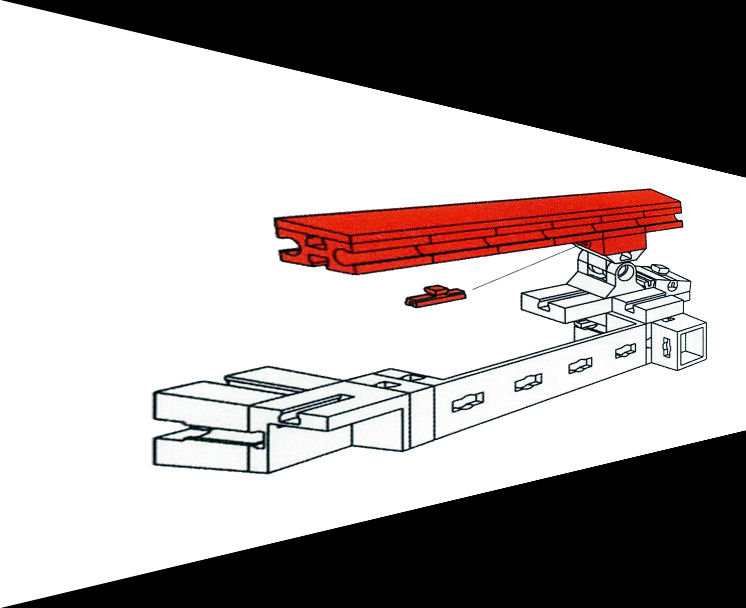
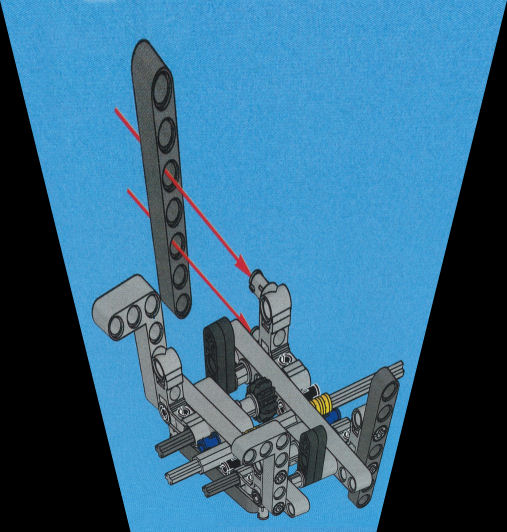
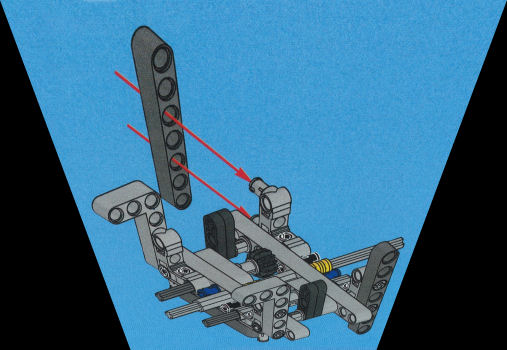
Die beiden Bilder 1.4 und 1.5 kommen aus gutem Grund nicht in den Originalbauanleitungen vor. Es sind näherungsweise zentralprojektiv verzerrte Darstellungen der Originalbilder, nur für diesen Text hergestellt (Bild 1.4 ist weniger gut gelungen, da die Fluchtpunkte nicht stimmen). Hier sind die Lochabstände nicht konstant, sondern verzerrt. Und ob die beiden "vertikalen" dunkelgrauen Lego-Stäbe in Bild 1.5 wirklich parallel oder etwa zueinander schräg verlaufen müssen, ist nicht mehr zu erkennen.

Bild 1.4 - 1.6

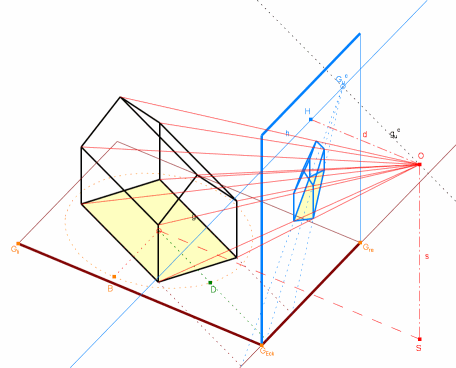
Die Bilder 1.7 und 1.8 zeigen den Unterschied zwischen Parallelprojektion und Zentralprojektion. Sie können unten auch die dynamische Version aufrufen, um das Haus zu drehen oder die Darstellungs- und Abbildungsgeometrie zu variieren.

Bild 1.7 - 1.8

2. Beispiel I: Technische Zeichnung / Buchillustration

Abschnitt überspringen

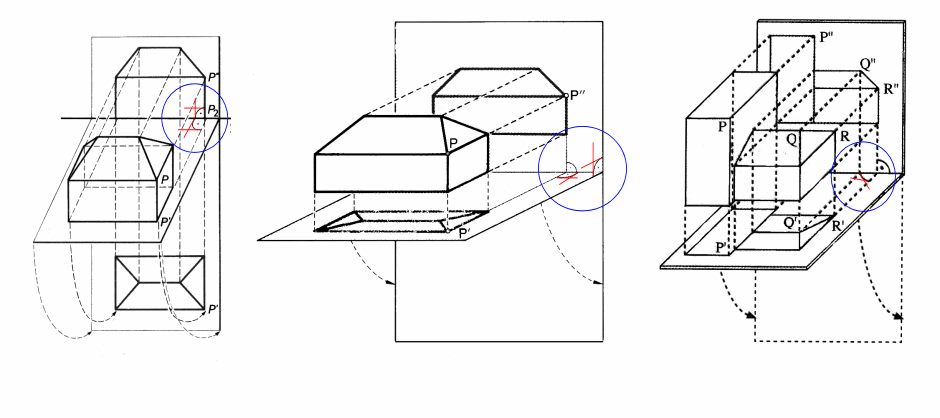
Die folgenden Bilder sind alten Schulbüchern über einen Zeitraum von zwei Dekaden entnommen. Hier geht es um die in der Technik weitverbreitete Zweitafelprojektion und es soll veranschaulicht werden, wie Grund- und Aufriss eines Hauses zusammenhängen. Dazu klappt man den Grundriß um 90° nach unten in die Aufrissebene; d.h., alle Grundrißpunkte wandern auf Viertelkreisen nach unten. Links in Bild 2.1 ist auch das Ergebnis zu erkennen, in der Mitte und rechts ist nur der Klappvorgang gezeigt. In welchem der Bilder wirkt der Klappvorgang am natürlichsten?

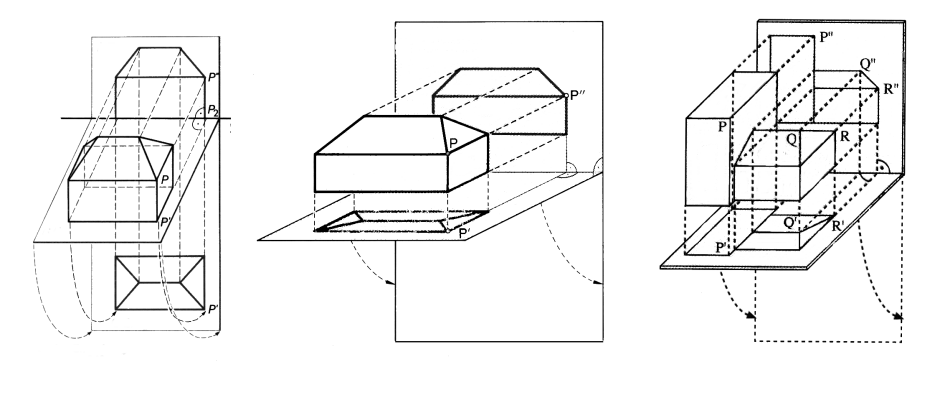
Bild 2.1

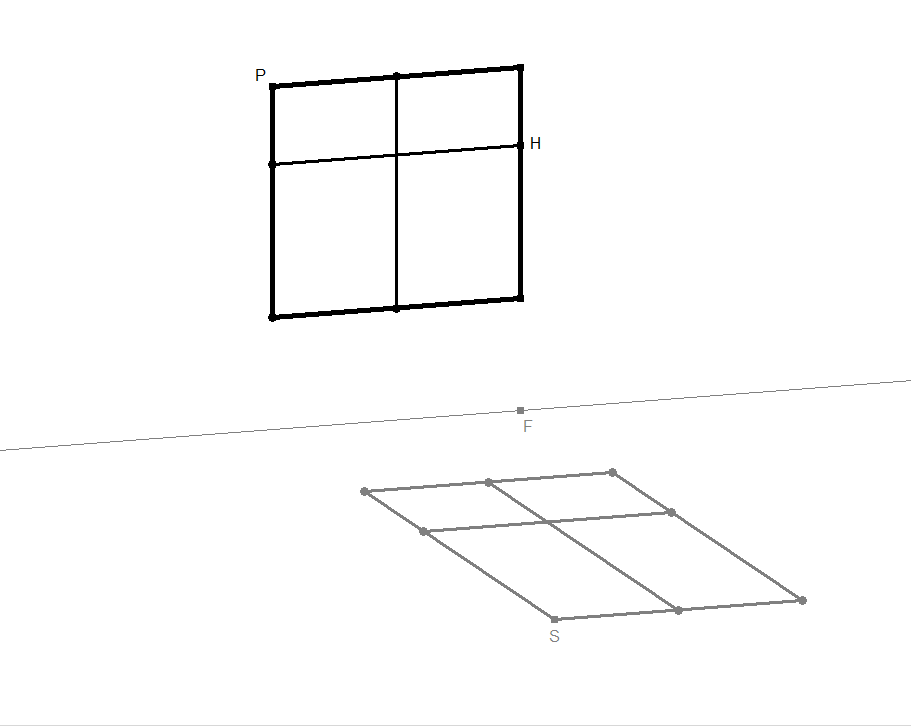
Damit die Entscheidung etwas leichter fällt, folgende Überlegungen: Denken Sie sich einen quadratischen Karton mit den beiden Mittelparallelen und dem Inkreis, der die Quadratseiten (Kartonkanten) dort berühren muss, wo die Mittel­parallelen durch gehen. Der Karton steht senkrecht auf dem Tisch, teils schräg gedreht. Könnte das wie folgt aussehen?

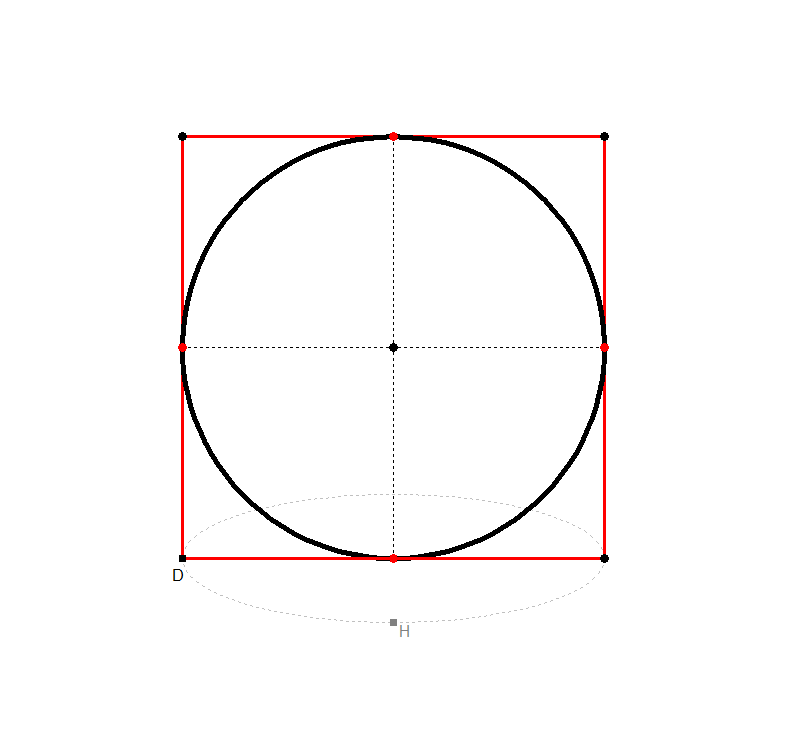
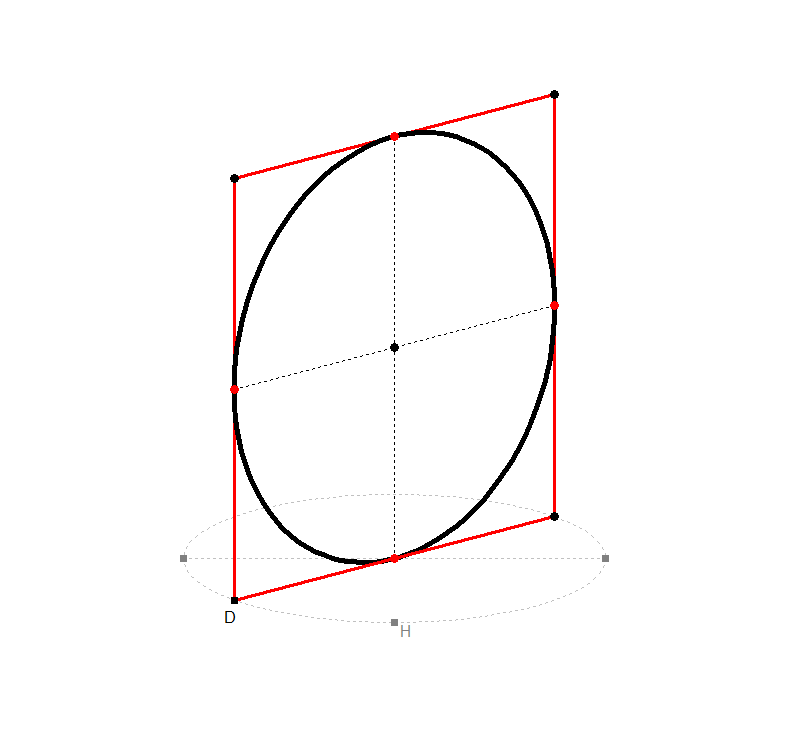
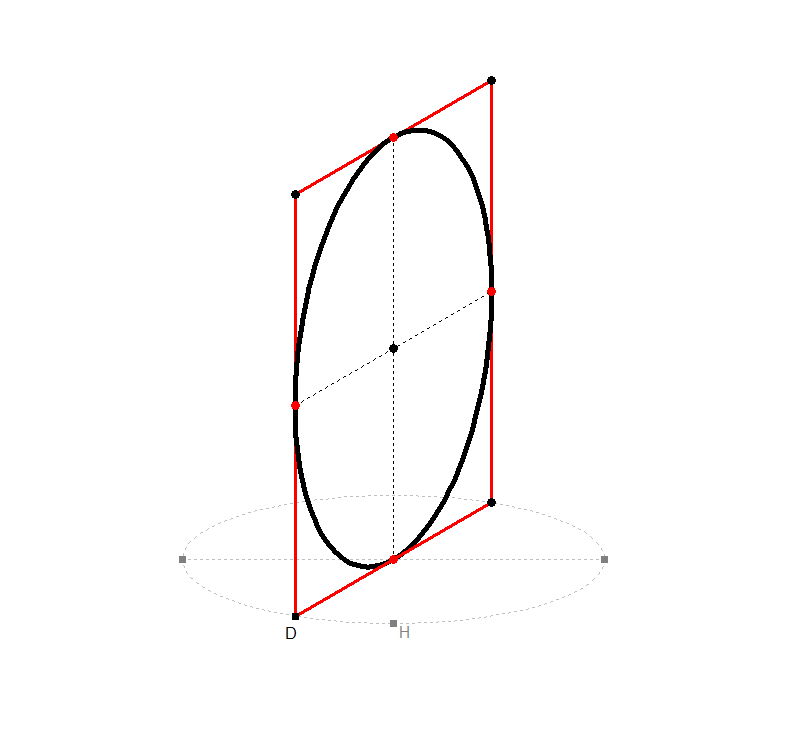
Bild 2.2a - 2.2c
 

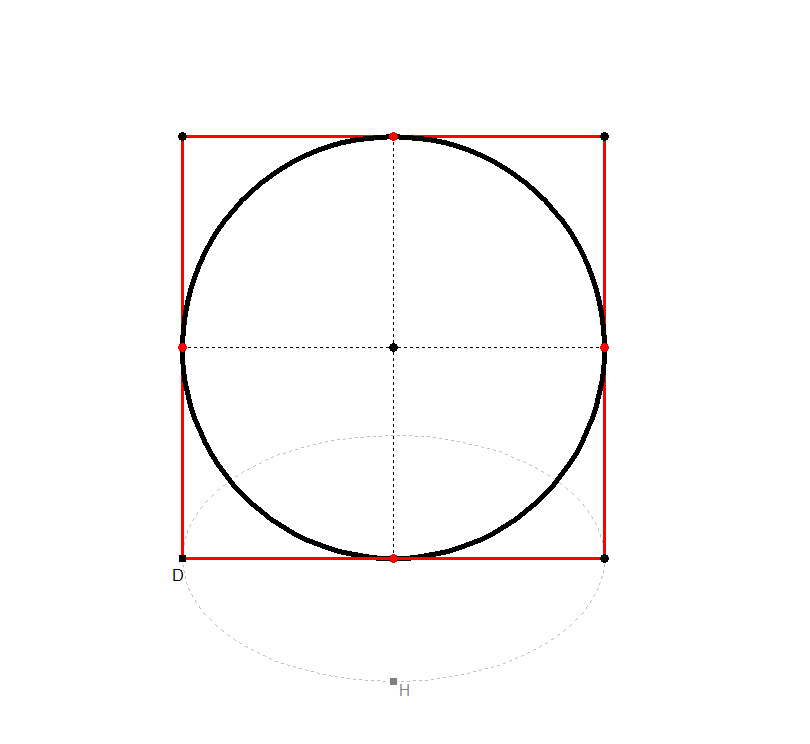
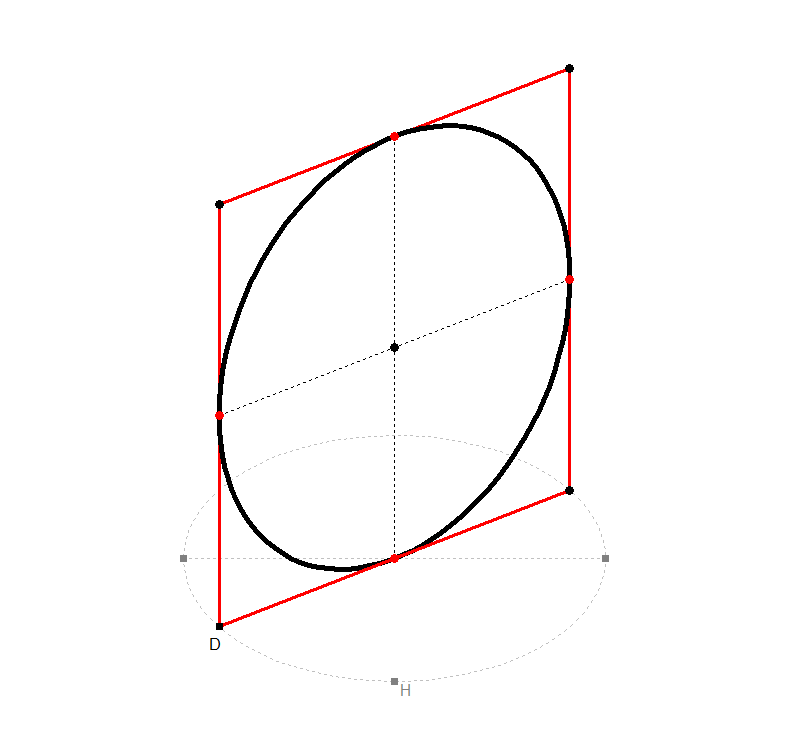
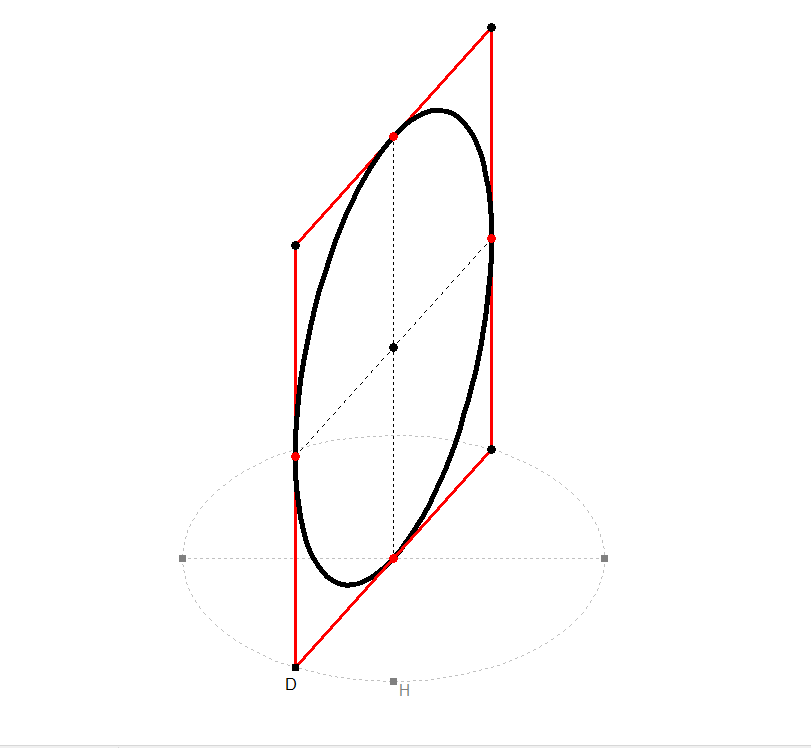
Bild 2.2d - 2.2f

Die Mittelparallelen des Quadrats sind zugleich die Berührdurchmesser der Tangenten des Inkreises. D.h., immer zwei gegenüberliegende Tangenten sind durch einen Berührdurchmesser verbunden mit der Folge, dass jede dieser Kreistangenten parallel ist zum jeweils anderen Berührdurchmesser (Berührradius). Mathematiker sprechen hier von konjugierten Durchmesser(paaren). Die beiden Berührdurchmesser teilen die Kreislinie in vier Viertelkreisbögen, denen vier Viertelellipsenbögen entsprechen.

Spielen Sie selbst mit dem Kreis durch Klick auf Bild 2.2d, ändern Sie seine Lage im Raum usw.

Wodurch unterscheiden sich die beiden Bilderreihen 2.2a - 2.2c und 2.2d - 2.2f?
Vergleichen Sie mit Bild 2.1; sehen Sie schon die Zeichenfehler?
Schauen Sie sich ggf. das folgende Bild 2.3 an:

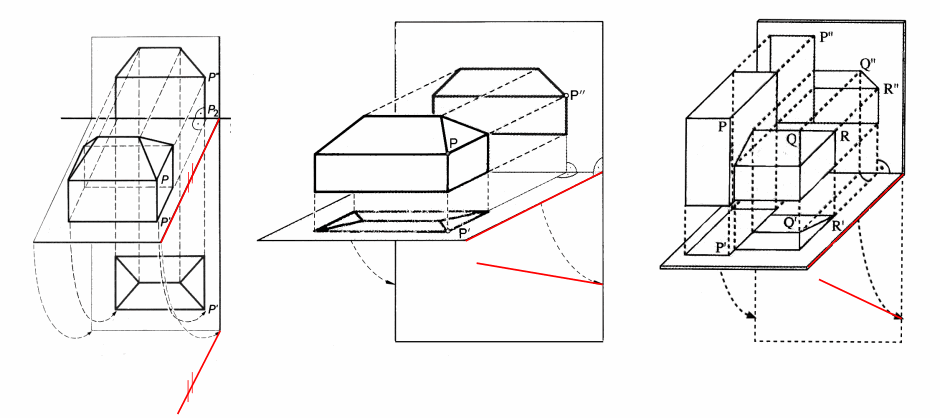
Bild 2.3

Links hat der Zeichner (im Rahmen der Zeichengenauigkeit) beachtet, das die Drehbögen der Anordnung Viertelkreisen entsprechen, deren Tangenten in den Endpunkten der Kreisbögen parallel zum zugehörigen anderen Berührradius sein müssen (konjugierte Durchmesser!), was sich offensichtlich auf die entsprechenden Ellipsenbögen überträgt. Im mittleren Bild hatte dies der Zeichner nicht beachtet und im rechten erst recht nicht.

Bild 2.4

Allerdings wusste der mittlere Zeichner sehr wohl, wie das mit den Schrägbildern von Viertelkreisen ist. Bei den kleinen Rechten Winkeln (blau eingekringelt) hat er die Schrägbilder richtig gezeichnet. Der rechte Zeichner hingegen hat sich ganz auf die Punkte konzentriert und nicht auf die Bögen.

3. Beispiel II: Schatten des Wohnzimmerfensters

Abschnitt überspringen

Die folgenden Fenster sind keine Hundertwasser-Fenster, sondern von solider schwäbischer Bauart. Will heißen, die Fensterrahmen sind geradlinig und bilden lauter rechte Winkel und die Fenstersimse sind waagrecht eingebaut.

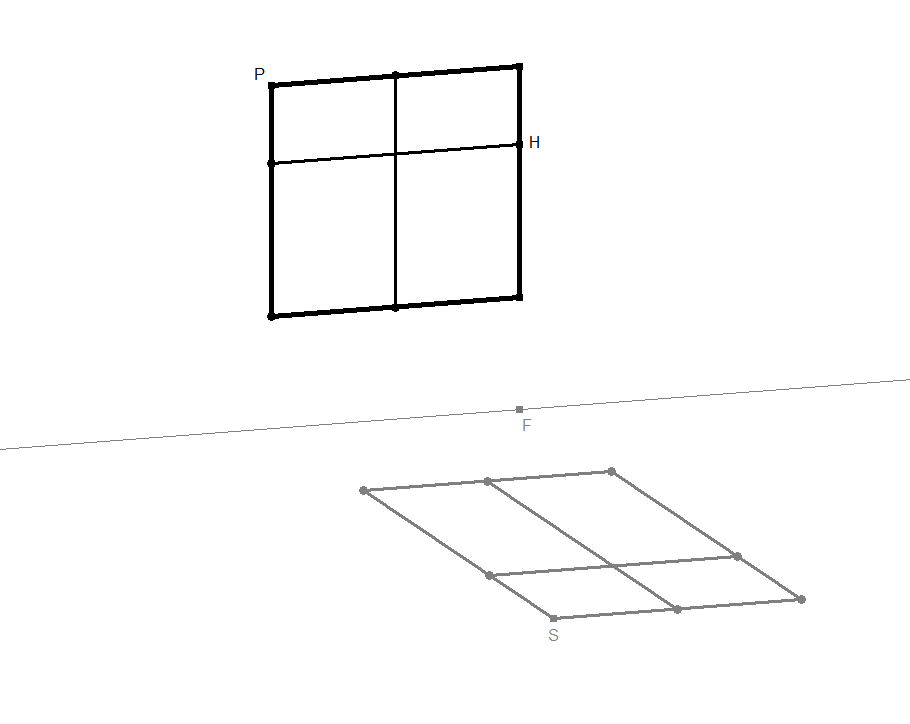
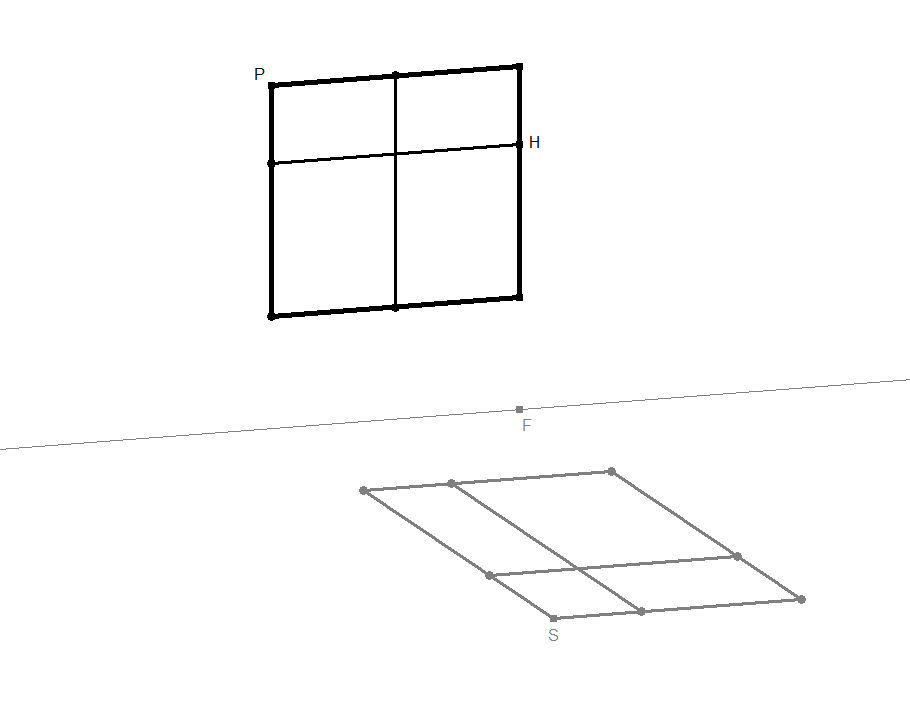
Die Sonne scheint herein und wirft auf dem Fußboden einen Schatten. Welches der Fenster 3.1a - 3.1c wirft einen realistischen Schatten. Warum sind die beiden anderen Schatten falsch?

Bild 3.1a - 3.1c

Was geschähe mit dem Schatten, wenn das Fenster breiter wäre, wenn es tiefer eingebaut wäre, wenn das Fensterkreuz eine andere Einteilung hätte? Welche Gesetzmäßigkeiten gelten also für den Schattenwurf eines sonnenbeschienenen Objektes?

Bild 3.2a - 3.2c

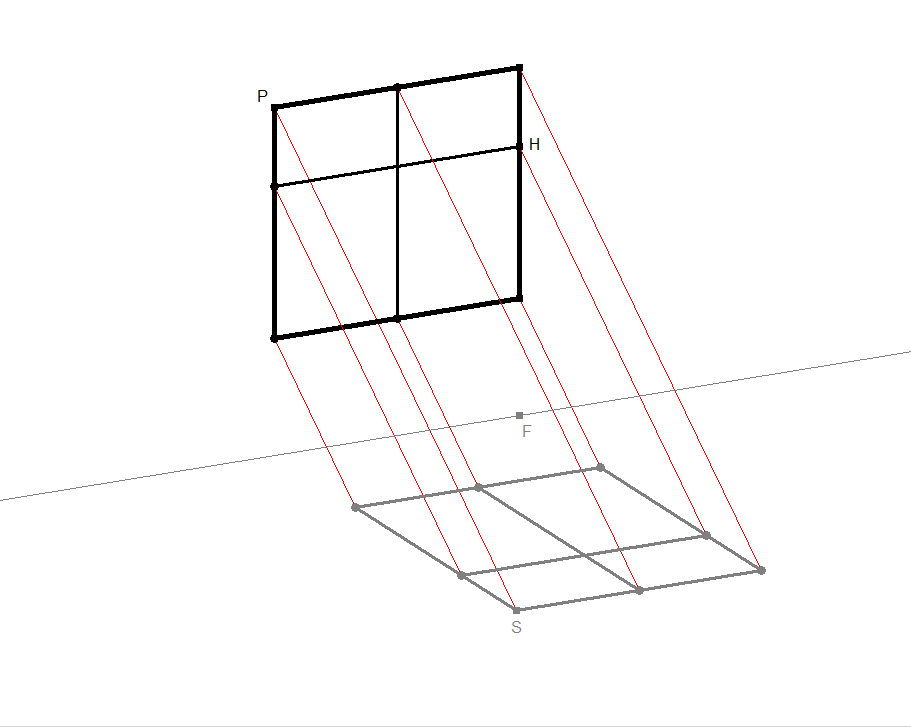
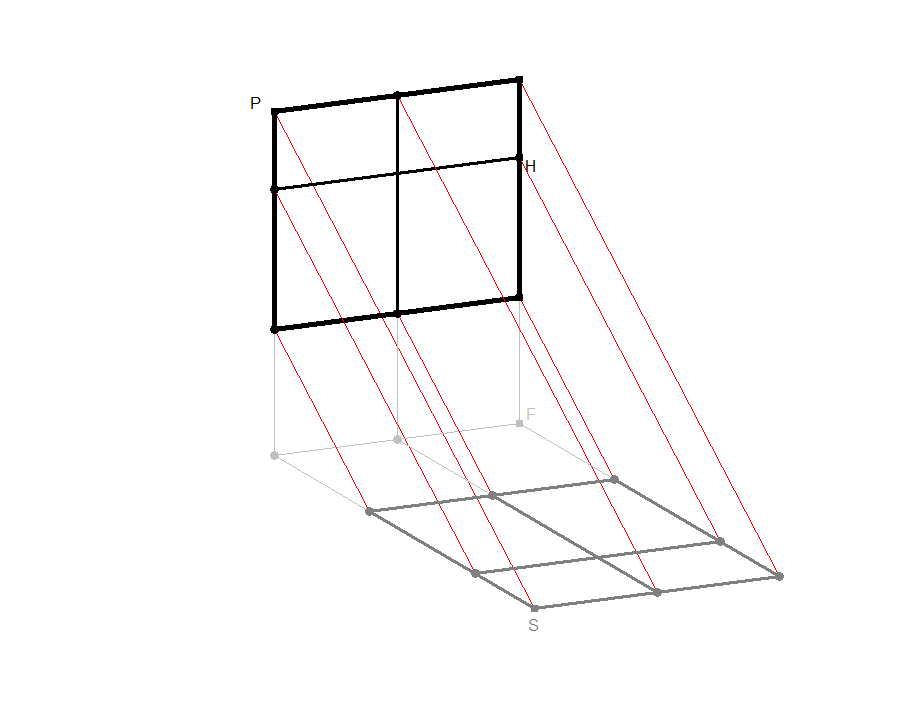
In den Bildern 3.2a - 3.2c werden der Reihe nach immer mehr Konstruktionsdetails eingeblendet.

Spielen Sie selbst mit dem Fensterschatten durch Klick auf Bild 3.2a, ändern Sie seine Lage im Raum usw.

4. Eigenschaften des Sonnenschattens

Abschnitt überspringen

Die Schatten des Wohnzimmerfensters sind durch die Sonne hervorgerufen, deren Licht aufgrund des großen Abstands zur Erde parallel einfällt. Daher entstehen die Schattenwürfe durch Parallelprojektion. Würden sie nachts durch eine einzelne Laterne entstehen, käme das Licht (näherungsweise) aus einem Zentrum und es läge Zentralprojektion vor, wie sie auch bei Fotoapparaten und Projektoren vorliegt. Man spricht in beiden Fällen von einer Abbildung des Raumes auf die Ebene.

In diesem Sinne ist der Sehvorgang im menschlichen Auge keine derartige Abbildung, denn im Auge wird der Raum auf eine Späre abgebildet (die Netzhaut). Freundlicherweise "rechnet" unser Hirn die Augapfelbilder so um, dass wir Geraden gerade sehen und nicht gekrümmt und Parallelen auch als parallel erkennen können! Ja, wir erkennen sogar, ob eine Tischplatte ein Rechteck ist, selbt wenn wir schräg drauf sehen.

Bei der Parallelprojektion von Objekten auf eine Ebene entstehen i.a. Schrägbilder. Diese Abbildung kennen wir alle von klein an; so wirft das sonnenbeschienene Kinderbettchen mit seinen Gitterstäben einen charakteristischen Schatten auf den Fußboden. Und dieser Schatten folgt einigen Gesetzmäßigkeiten:

1. Punkttreue: Jeder Urpunkt wird auf einen Bildpunkt abgebildet. Die ist selbsverständlich (wenn Licht im Spiel ist).

2. Geradentreue: Jede Urgerade wird auf eine Bildgerade abgebildet (wenn die Urgerade nicht projizierend ist). Diese Geradentreue bedarf der Hervorhebung; sie gilt zwar auch bei normalen Fotoapparaten, aber schon nicht mehr bei Fischaugenkameras!

3. Parallelentreue und Teilverhältnistreue: Sind die Urgeraden parallel, so sind es auch deren Bildgeraden; das Teilverhältnis dreier Urpunkte auf einer Urgeraden bleibt auch für deren Bilder erhalten. Beide Eigenschaften sind mathematisch eine Folge der Strahlensätze und daher nicht unabhängig voneinander (sie bedingen sich gegenseitig).

Beide Eigenschaften von 3. werden schön im Beispiel II beim Fensterschatten gezeigt. Die Kurzform der Teilverhältnistreue lautet: Mitte bleibt Mitte, was wegen der Zentralprojektion nicht für Fotoapparate gilt: der Mittelpunkt der Bildellipse eines Kreises ist auf einem Foto i.a. nicht das Bild des Kreismittelpunktes!

Derartige Abbildungen (also solche mit den Eigenschaften 1 - 3) heißen Affinitäten. Offensichtlich werden Längen und Winkel bei der Parallelprojektion geändert (und damit auch Flächeninhalte), sind also keine affinen Eigenschaften (Mathematiker sagen, das seien euklidische Eigenschaften).

Beim Kinderbettchen in der Sonne werden im engeren Sinn (mehrere) Ebenen (des Raumes), nämlich die Seitenwände des Bettchens, auf die Ebene (den Fußboden) abgebildet. Es handelt sich also um mehrere Abbildungen jeweils einer Ebene (Seitenwand) auf eine andere (Fußboden) oder eine dritte (Zimmerwand). Das sind also räumliche Parallelprojektionen einer Ebene auf eine andere. In den Beispielen I und II sind Bilder auf eine Bildebene "gemalt"; es gelten aber die gleichen Eigenschaften 1 - 3 (und noch einige andere). Diese ebenen Affinitäten (Affinitäten der "Bildebene" auf sich selbst) sind also Bilder räumlicher Affinitäten. Verwirrt? Kinder, die Bilderbücher ansehen, verstehen das auf Anhieb.

Bild 4.1 - 4.2

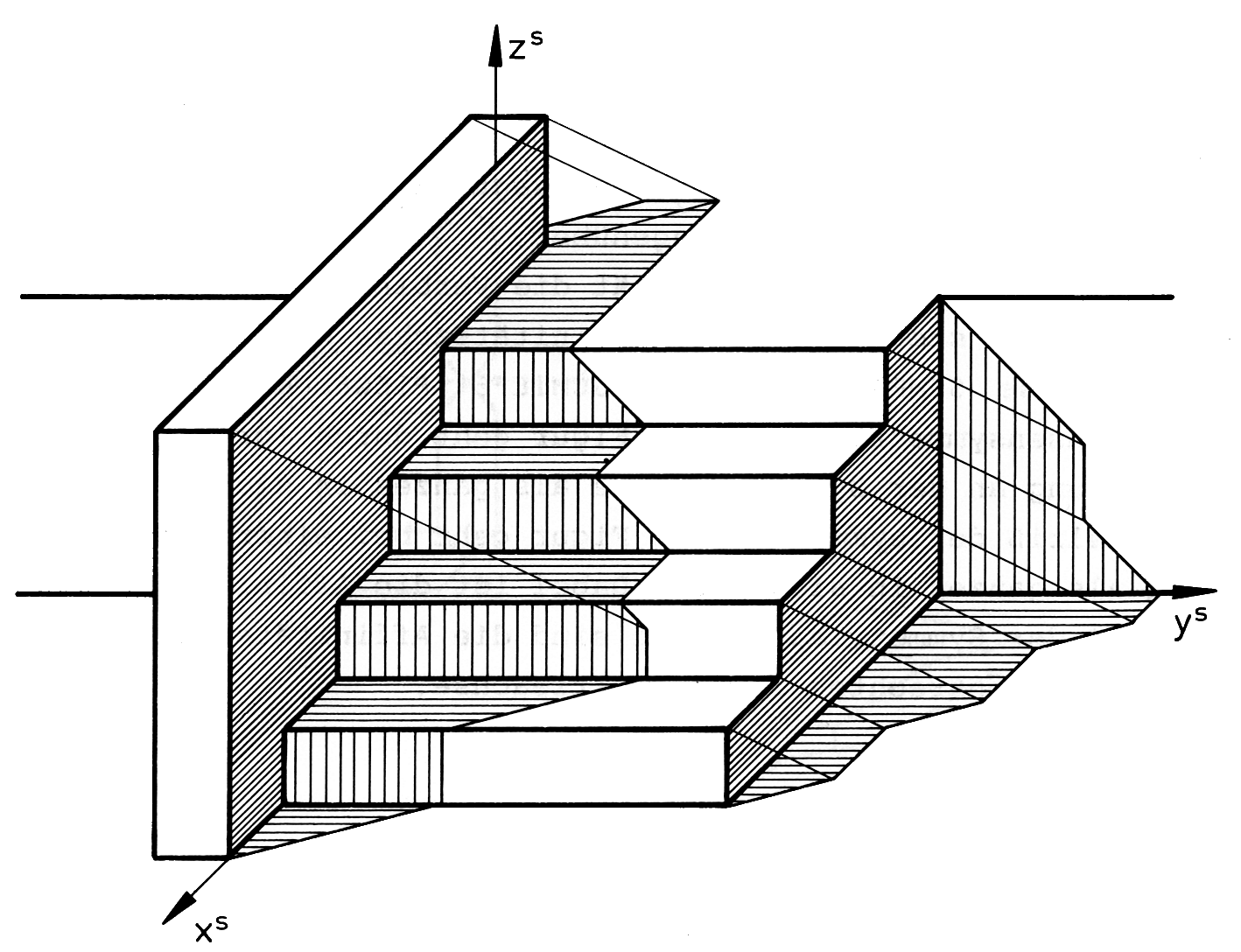
Ein schönes Beispiel stellt in Bild 4.1 der Schattenwurf einer Treppe^*) mit mehreren schattenwerfenden und mehreren schattenfangenden Ebenen dar.

Die beiden Beispiele I und II weisen noch weitere Eigenschaften auf. Am Fens­ter­schatten in Bild 4.2 ist dies besonders leicht nach zu vollziehen:
Wenn man die Fensterunter­kante nach unten verschiebt, ist spätestens Schluss bei der Zimmerkante; deshalb ist diese im Bild rot hervorgehoben. Senkt man also den Sims bis zum Boden ab, dann wandert dessen Schatten nach hinten auf die Fensterwand zu, spätestens an der roten Kante ist Schluss; beide fallen auf der roten Kante zusammen, das linke Eck mit dessen Schatten, das rechte mit dessen Schatten und der Fensterkreuzfußpunkt mit seinem Schatten. Wenn also das Fenster bodentief eingebaut wäre, würde jeder Punkt der Unterkante mit seinem Schatten zusammenfallen. Die ganze Kante fällt Punkt für Punkt mit ihrem Schatten zusammen; jeder Punkt der Kante ist Fixpunkt, sie ist also die Fixpunktgerade oder Achse dieser Affinität, es liegt somit eine Achsen­affinität vor. Die im Bild grün eingezeichneten Sonnenstrahlen heißen nun Affinitätsstrahlen. Damit ergibt sich Eigenschaft 4:

4. Jede Urgerade schneidet ihre Bildgerade auf der Achse (oder ist samt Bildgerader parallel zur Achse) und alle Affinitätsstrahlen (Verbindungsgeraden Urpunkt - Bildpunkt) sind parallel zueinander. Beide Aussagen sind wieder äquivalent, wie schon die beiden von Eigenschaft 3.

Gelten die Eigenschaften 1 - 4, so liegt eine Achsenaffinität vor (perspektive Affinität, Parallelstreckung, Parallelstau­chung).

5. Achsenaffinitäten

Abschnitt überspringen

Bei den Fenstern von Beispiel II liegen die Urpunkte auf der einen, deren Bildpunkte auf der anderen Seite der Achse. Da die Fenster aus Geraden(teilen) aufgebaut sind, die deren Bilder auf der Achse schneiden (müssen), können wir uns auch die ganzen Geraden denken, die dann zwangsläufig die Achse überqueren müssen. Dann sieht das Ganze zwar nicht mehr wie ein Fenster samt Schatten aus, bleibt aber gleichwohl eine Achsenaffinität. Man könnte den Lichtweg auch umkehren. Nur müsste die Sonne dann von unten scheinen, was wohl nur mit Tricks möglich wäre (z.B. Umlenk­spiegel).

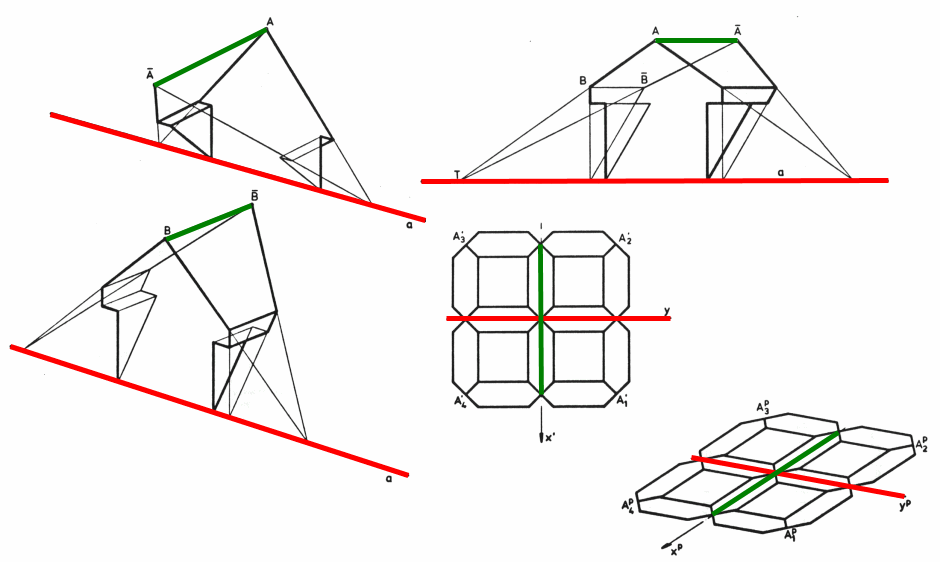
Daher sind im folgenden Bild^*) einige andere Achsenaffinitäten vorgestellt, bei denen ganz auf die Sonne verzichtet werden kann.

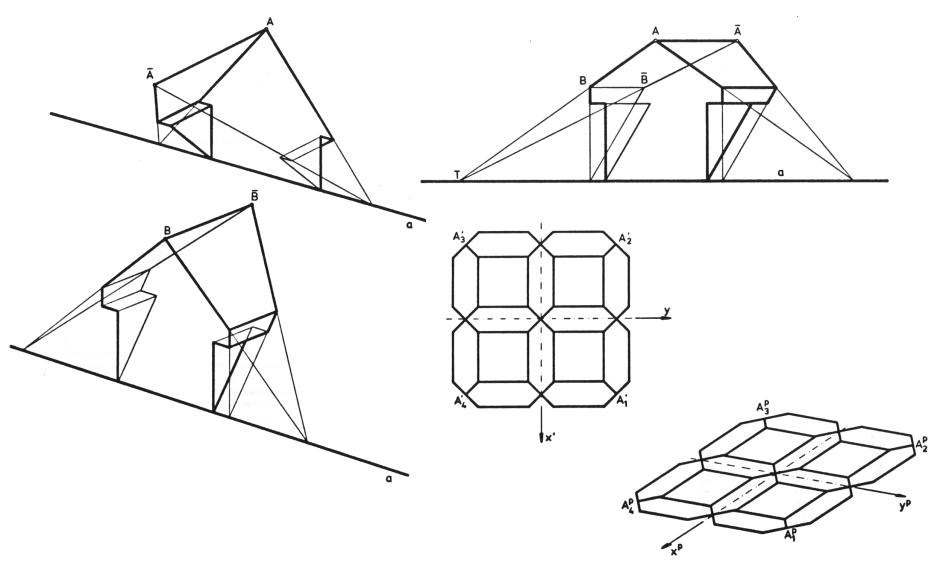
Bild 5.1

Links sind zwei schiefe Achsenaffinitäten dargestellt, oben werden die Punkte in Richtung auf die Ache abgebildet (Parallelstauchung), unten von der Achse weg (Parallelstreckung). In der Scherung rechts oben bewegen sich die Punkte parallel zur Achse; in der Mitte ist eine Achsenspiegelung dargestellt und rechts unten eine Schräg­spiegelung.

Bild 5.2

Die Achse (Fixpunktgerade) ist jeweils rot gekennzeichnet, die Affinitätsrichtung (Fixgeraden) grün. Bei den beiden Spiegelungsarten sind die rote und die grüne Gerade austauschbar. Sie könnten als Parkett und Schrägbild des Parketts realisiert sein. Die anderen Achsenaffinitäten könnten Achitektenzeichnungen von Dachgauben sein.

Spielen Sie dynamisch mit einer Dachgaube durch Klick auf ; verwandeln Sie die schiefe Achsenaffinität in eine Scherung usw.

Die linke obere Dachgaube erscheint von der Sraße aus links unten vor dem Haus stehend betrachtet zu werden. Die Dachgaube darunter erscheint vom rechts gegenüber liegenden Haus von einem höheren Stockwerk aus betrachtet zu werden. Aber wo befindet sich der Betrachter der rechten Dachgaube? Deren Firstlinie (AA)und die Dachrinne (Achse a) verlaufen in unterschiedlichen Höhen waagrecht unter 90° zueinander (also windschief zueinander). Wäre der Betrachter auf Höhe der Firstlinie, dann sähe er die tatsächlich waagrecht, aber die Dachrinne müsste schräg zu sehen sein. Wäre er aber auf Höhe der Dachrinne, sähe er diese waagrecht und die Firstlinie schräg. Das liegt daran, dass wir beim Betrachten von Objekten Zentralprojektion verwenden und keine Parallelprojektion.

Sind das alle denkbaren Typen von Achsenaffinitäten; kann man jede durch ein Sonnenschattenmodell erklären? Gibt es Affinitäten ohne Achse?

6. Typisierung der Affinitäten

Abschnitt überspringen

Will man solchen Gesetzmäßigkeiten auf den Grund gehen, dann helfen die Disziplinen der analytischen und der darstellenden Geometrie weiter. Die analytische Geometrie liefert die (abstrakte) Klassifizierung der Affinitäten und die darstellende Geometrie liefert die Anschauung und Konstruktionsdetails.

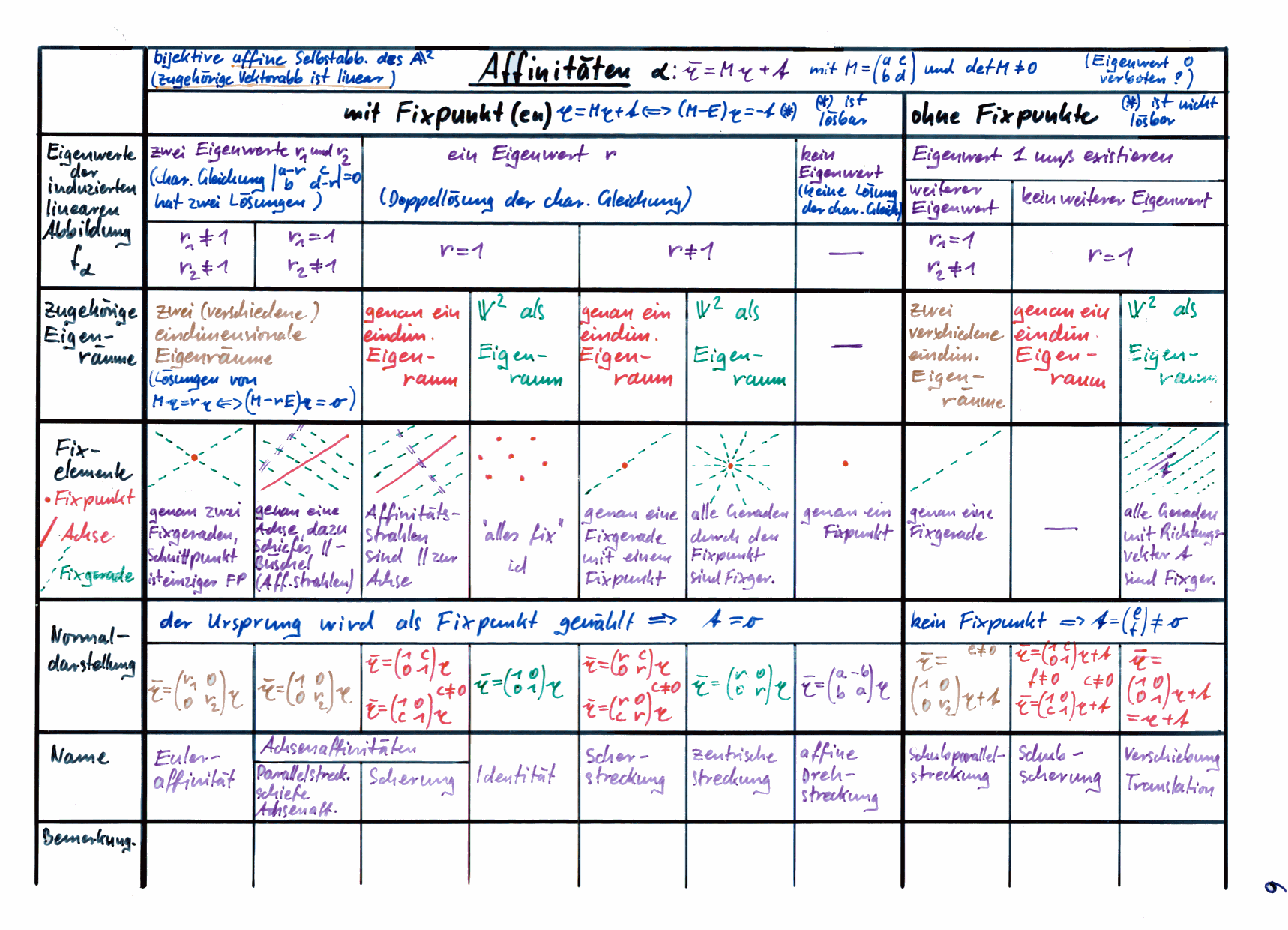
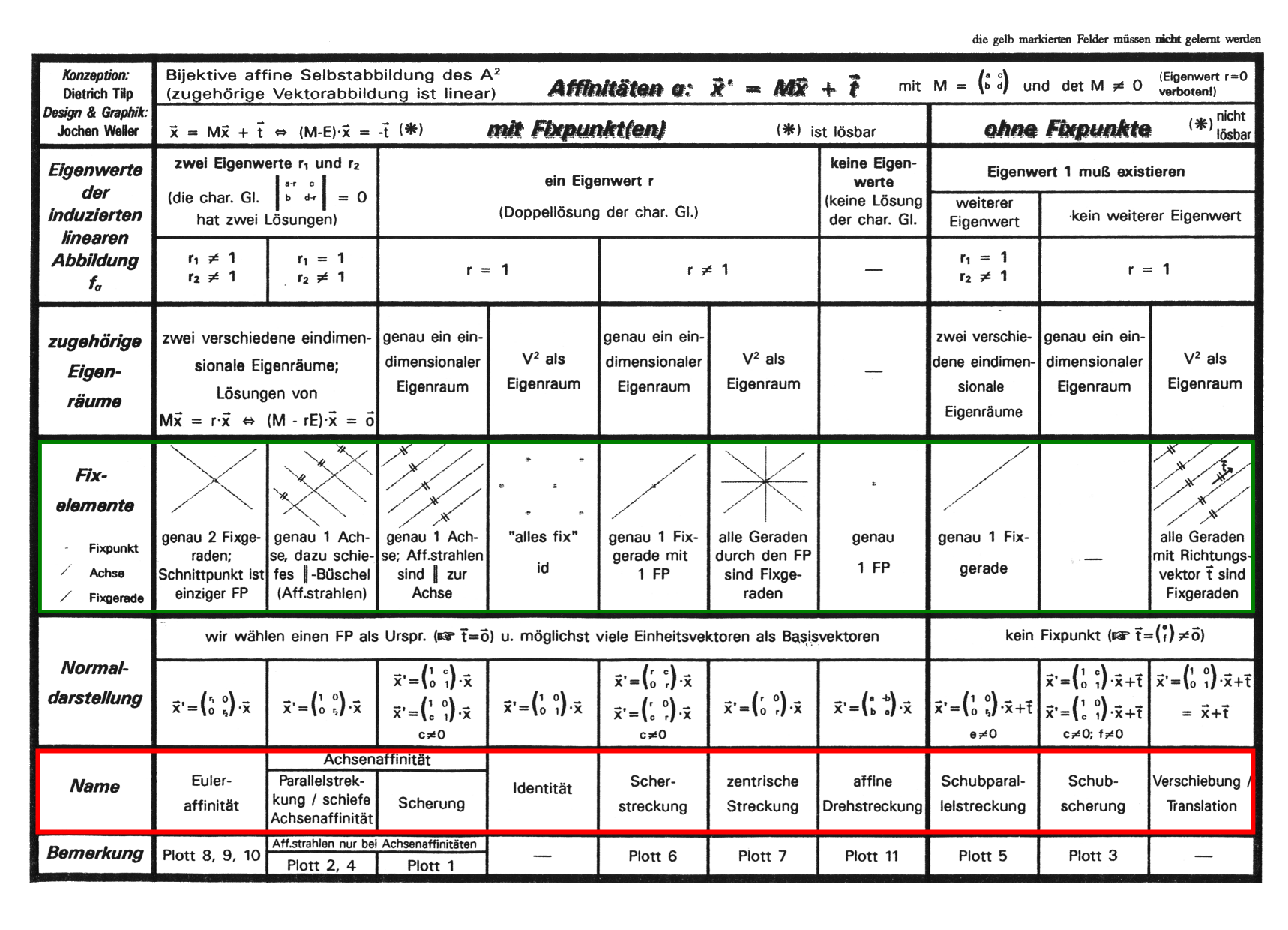
Auf der folgenden Folie passt die komplette Klassifizierung aller Affinitäten samt Herleitung komprimiert auf eine DIN-A4-Seite.

Bild 6.1

Der Folie ist anzusehen, dass sie schon zu Beginn der Achziger erstellt worden war, damals haben wir im Unterricht Vektoren noch in Sütterlin geschrieben. Im LK Mathematik 1992-94 hat Jochen Weller dankenswerterweise die Folie in Word übernommen und dabei die Schreibweise modernisiert:

Bild 6.2

Hier soll zunächst nur der rot markierte Bereich interessieren, in dem die Ergebnisse zusammengefasst sind (die math. Details, die zu diesen Ergebnissen führen, sind in Abschnitt 11 zusammengefasst). Offensichtlich gibt es viel mehr Affinitäten, als die obigen Abschnitte vermuten ließen.

Die schiefen Achsenaffinitäten werden auch als Parallelstreckungen bezeichnet (in Abgrenzung zu zentrischen Streckungen); sie umfassen auch die Sonderfälle Achsenspiegelung und Schrägspiegelung. Sie bilden aber zusammen mit der Scherung (als parallele Achsenaffinität) die Minderheit im Konzert aller Affinitäten. Allerdings sind sie darstellend geometrisch leicht beherrschbar.

7. Beispiele zur Typisierung

Abschnitt überspringen

Jeder Abbildungsname in Tabelle 6.2 scheint "sprechend" zu sein; man kann sich denken, was bei der einzelnen Abbildung passieren muss. So glaubt man, sich vorstellen zu können, was eine Schubparallelstreckung sein soll, nämlich die Verkettung (Hintereinanderausführung) einer Parallelstreckung und einer Verschiebung. Und die Drehstreckung entsteht wohl aus einer (zentrischen) Streckung mit anschließender Drehung (oder umgekehrt?). Nur die Euler-Affinität verät im Namen nicht, was gemeint sein könnte. Aber auch für die anderen nicht axialen Affinitäten gibt es (zunächst) keine einfachen Konstruktionsrezepte.

Daher werden im Folgenden zunächst alle Affinitäten anhand einer einfachen Urfigur (Kirche) samt Bild vorgestellt. Im anschließenden Abschnitt werden wir dann versuchen, die nicht axialen Affinitäten mittels Verkettung zu erschließen. Der grün markierte Bereich in Bild 6.2 wird wichtigen Aufschluss zu Klassifizierung liefern. Dort ist abzulesen, welche Affinitäten eine Achse besitzen und welche nicht. Allerdings haben wir bisher nur solche mit Achse kennengelernt. Haben die nicht axialen Affintäten keine praktische Bedeutung?

Die Vorlagen sind dem Vortrag von 1985 entnommen, sie wurden damals mittels eines kleinen Turbopascalprogramms erstellt.

Die ersten drei Bilder 7.1a - 7.1c stellen weitere Parallelsteckungen dar, eine schiefe Achsenaffinität, eine ""senkrechte" Achsenaffinität und eine parallele Achsenaffinität (Scherung).

Bild 7.1a - 7.1c

Die folgenden drei Bilder 7.2a - 7.2c stellen Euler-Affinitäten dar. Wie wir noch sehen werden, sind das Verkettungen zweier geeigneter Parallelstreckungen.

Bild 7.2a - 7.2c

Die nächten beiden Bilder 7.3a - 7.3b stellen eine zentrische Streckung und eine Drehstreckung dar.

Bild 7.3a - 7.3b

Es folgen in Bild 7.4a - 7.4c Scherstreckung (Streckscherung), Schubparallelstreckung und Schubscherung.

Bild 7.4a - 7.4c

Der Vollständigkeit halber seien die Identität und die Translation (Parallelverschiebung) als Sonderfälle der Affinitäten aufgeführt; sie bedürfen keiner Darstellung.

8. Fixelemente von Affinitäten

Abschnitt überspringen

Auf die Begriffe Achse und Affinitätsstrahl (Affinitätsrichtung) muss noch eingegangen werden, denn die dienen der Klassifizierung aller Affinitäten, wie der Tabelle 6.1 zu entnehmen war. Um ein gegebenes Objekt einer Achsenaffinität unterziehen zu können, müssen nämlich drei Angaben gemacht werden:

• Erstens muss die Achse vorgegeben sein. Auf ihr liegen alle Urpunkte, die mit ihrem Bildpunkt zusammenfallen, die also Fixpunkte sind; die Achse bleibt also punktweise fix (kein Punkt der Achse wird beim Abbilden wegbewegt) und heißt daher auch Fixpunktgerade (manche sagen auch Punktfixgerade).

• Zweitens muss die Richtung vorgegeben werden, in die alle Objektpunkte (außer denen der Achse) bewegt werden sollen. Diese Affinitätsrichtung wird durch Angabe einer Geraden mit eben der gewünschten Richtung dargestellt. Liegen mehrere Objektpunkte auf derselben derartigen Geraden, so werden deren Bilder wieder auf der Geraden landern, nur an anderen Stellen, also nicht auf den Urbildern. Punkte auf einer solchen Geraden können die Gerade nicht verlassen; wird eine solche Gerade als ganzes abgebildet, so bleibt deren Lage erhalten, obwohl sich deren Punkte bewegen, sie bleibt also fix (aber nicht punktweise), ist also eine Fixgerade (nicht aber eine Fixpunktgerade).

• Drittens muss festgelegt werden, wie weit die Objektpunkte (außer denen der Achse) gestreckt, also von der Achse weg bewegt, oder gestaucht, also auf die Achse zu bewegt werden sollen (Affinitätsfaktor). Je weiter ein Punkt von der Achse entfernt ist, desto stärker wird der Effekt sein. Aufgrund der oben erwähnten Eigenschaften 1 - 4 genügt es, von einem einzigen Urpunkt den zugehörigen Bildpunkt anzugeben (damit hat man auch die Affinitätsrichtung, also erübrigt sich die zweite Angabe), der Rest erfolgt konstruktiv.

Laut Tabelle 6.1 gibt es auch Affinitäten ohne Achse, also genügt offensichtlich der Blick auf die Fixelemente einer Affinität, um deren Typ zu bestimmen (Details s. Abschnitt 11):

• Zu Affinitäten mit (einer ganzen) Fixpunktgerade (Achse) gehören immer (viele zueinander parallele) Fixgeraden (Parallelstreckung, Scherung).

• Affinitäten mit (einem einzigen) Fixpunkt haben entweder ganz viele durch den Fixpunkt gehende Fixgeraden (zentrische Streckung) oder genau zwei sich im Fixpunkt schneidende Fixgeraden (Euler-Affinität) oder genau eine durch den Fixpunkt gehende Fixgerade (Scherstreckung) oder gar keine Fixgerade (Drehsteckung).

• Affinitäten ohne Fixpunkt haben entweder genau eine Fixgerade (Schubparallelstreckung) oder gar keine Fixgerade (Schubscherung).

9. Einführung der Verkettung von Abbildungen

Abschnitt überspringen

Am Ende von Abschnitt 1 sind Baugruppen von Fischer-Technik und Lego-Technik perspektiv verzerrt dargestellt worden (Bilder 1.3 und 1.4), um zu zeigen, dass eine derartige Zentralprojektion für technische Detailpläne weniger geeignet ist, als die deshalb in der Technik vorherrschende Parallelprojektion.

Nun wird gezeigt, wie diese Verzerrungen als Verkettung (Hintereinanderausführung) zweier einfacher linearer Abbildungen (Kollineationen) mit Hilfe eines Bildbearbeitungsprogramms erzeugt worden waren. Jeweils das zweite Bild (9.1b und 9.2b) stellt das Urbild (Original) aus der entsprechenden Bauanleitung dar, daneben ist das daraus erzeugte erste Abbild (9.1c und 9.2c) angegeben und das aus dem ersten Abbild erzeugte zweite Abbild (9.1d und 9.2d). Im zweiten Abbild wurden anschließend die schwarzen Flächen gefüllt, das dadurch entstandene Endprodukt (9.1a und 9.2a) ist zur besseren Vergleichbarkeit links neben dem jeweiligen Original dargestellt.

Bild 9.1a - 9.1d

Das erste Abbild entsteht jeweils durch horizontale bzw. vertikale "Perspektivverzerrung" (das entspricht der Zentralprojektion), das zweite durch Stauchen in horizontaler bzw. vertikaler Richtung (das entspricht senkrechter Achenaffinität).

Bild 9.2a - 9.2d

Derartige Abbildungen können beliebig oft hintereinander ausgeführt (verkettet) werden. Wir werden aber im Folgenden bei den Affinitäten bleiben und beobachten, welche Abbildungen entstehen, wenn man z.B. zwei verschiedene Achsenaffinitäten verkettet.

10. Verkettung von Affinitäten

Abschnitt überspringen

Verkettung zweier beliebiger Achsenaffinitäten

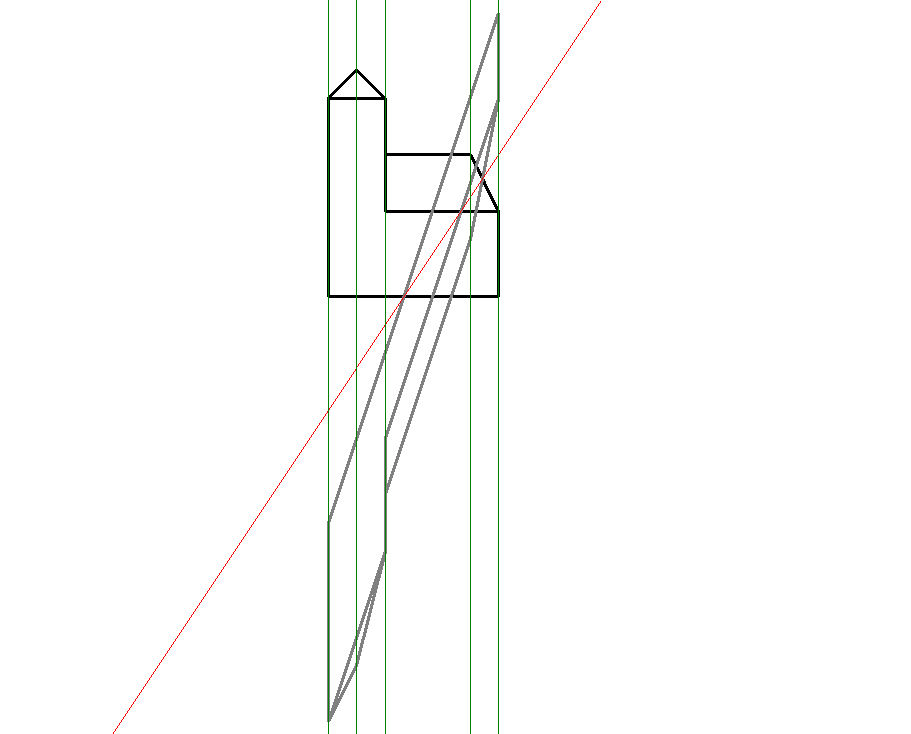
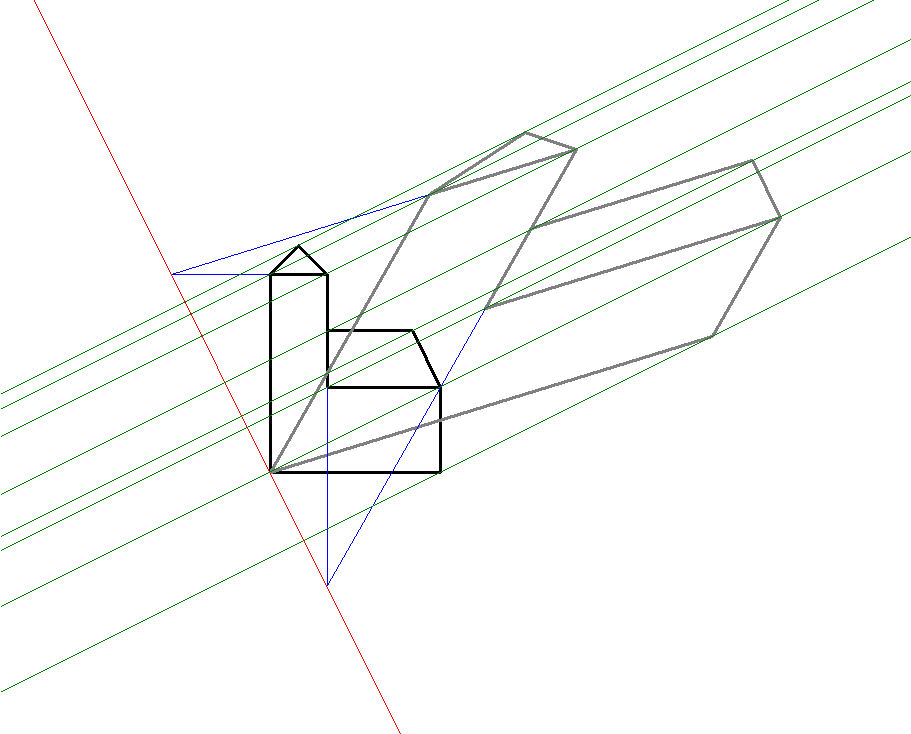
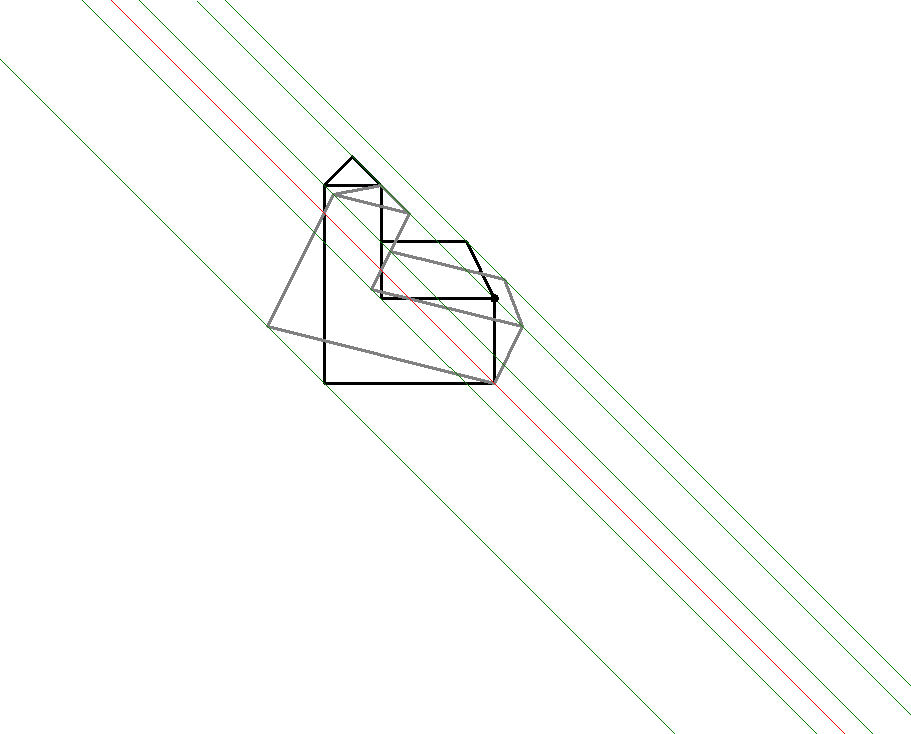
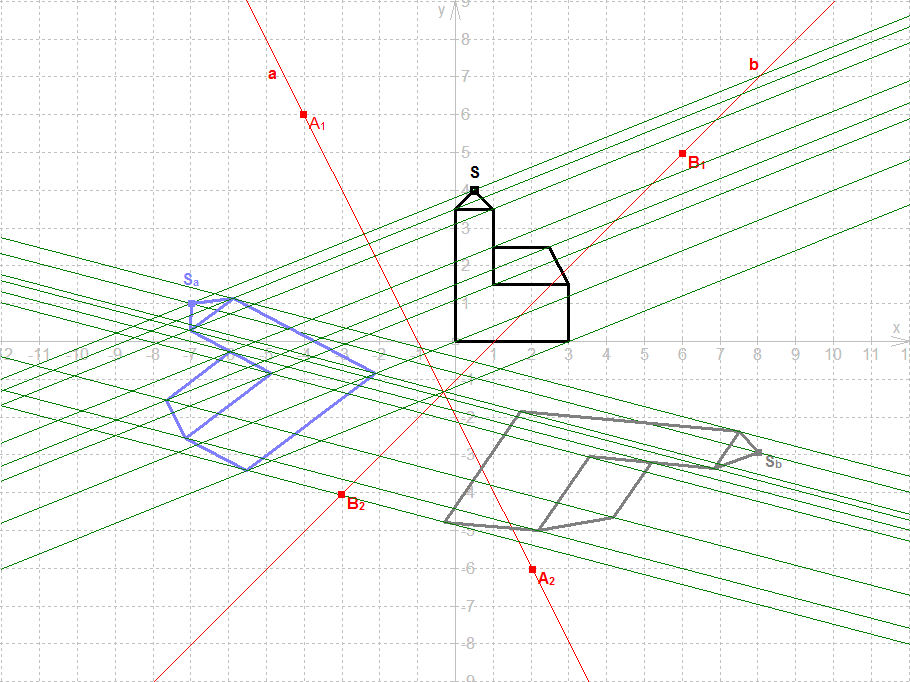
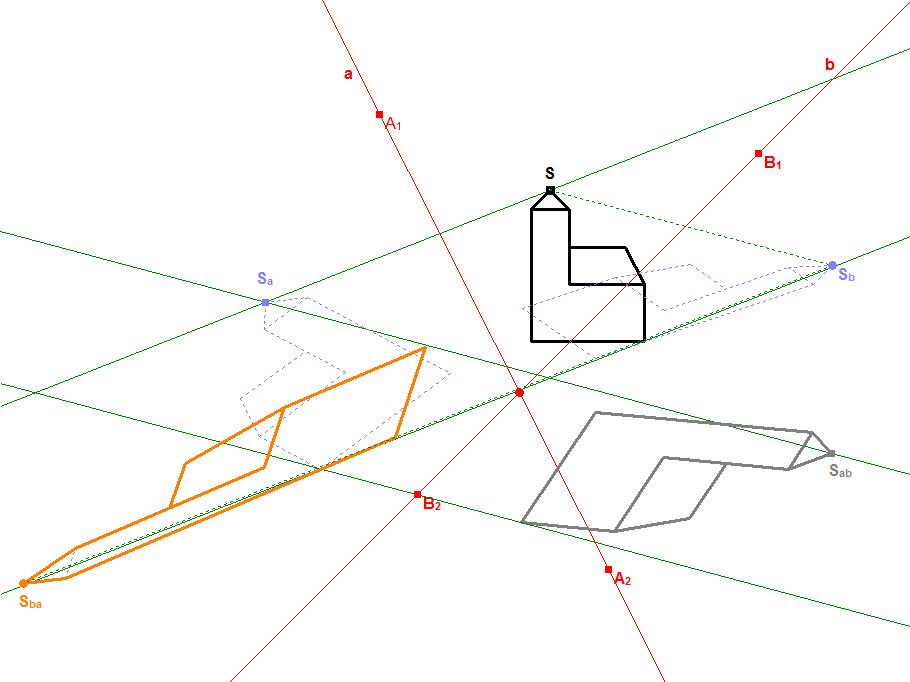
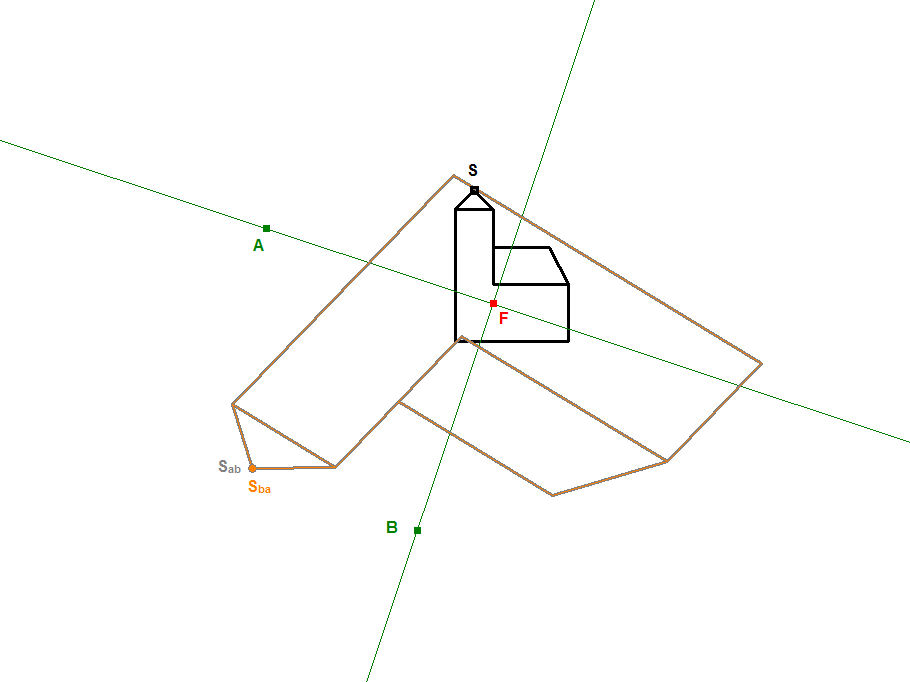
In jedem der folgenden Bilder wird die schwarze Kirche mittels a-Achsenaffinität auf die blaue Kirche abgebildet und diese anschließend mittels b-Achsenaffinität auf die graue Kirche.

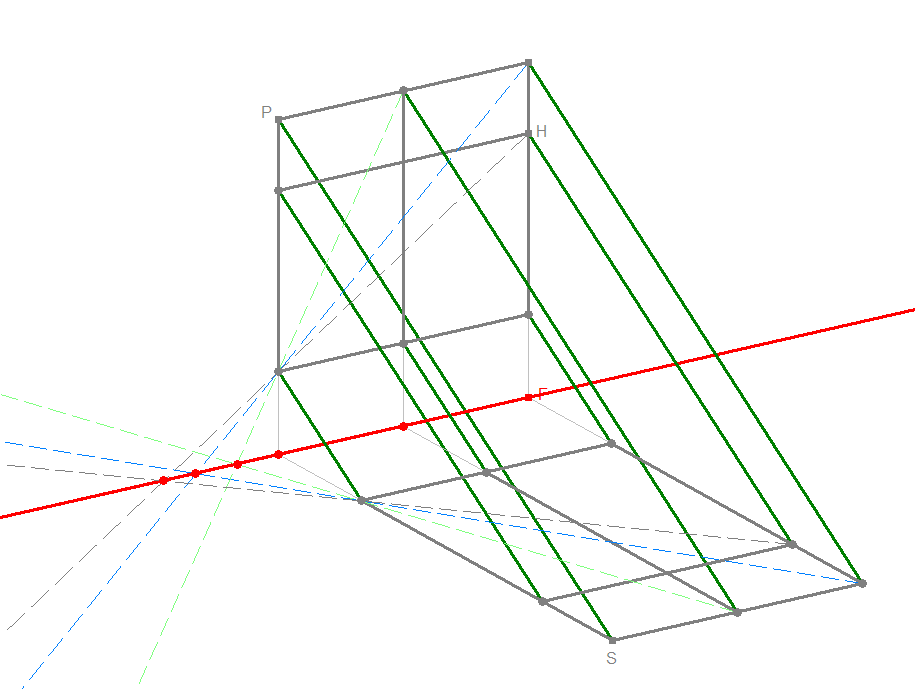
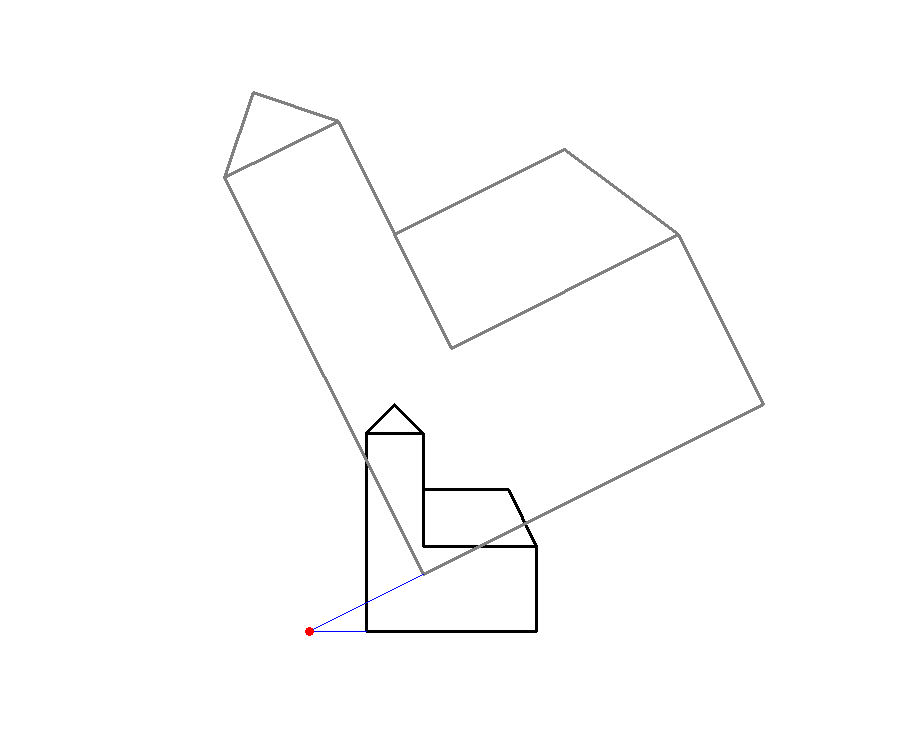
Die schwarze Kirche ist fest vorgegeben; von der a-Achsenaffinität ist die Achse a=A₁A₂ vorgegeben und das Bild S_a der Ur-Kirchturmspitze. Von der b-Achsenaffinität ist die Achse b=B₁B₂ vorgegeben und das Bild S_b vom Urbild S_a. Aus diesen Angabe berechnet DynaGeo die beiden Abbildungsgleichungen und erstellt damit der Reihe nach die beiden Bilder. Das tolle dabei ist, dass Sie durch Bewegen der Punkte A₁, A₂, B₁ und B₂ die Achsen bewegen können und durch Bewegen der Punkte S_a und S_b die Lage der jeweiligen Bilder beeinflussen können, wobei DynaGeo in Echtzeit die Bilder neu berechnet und darstellt.

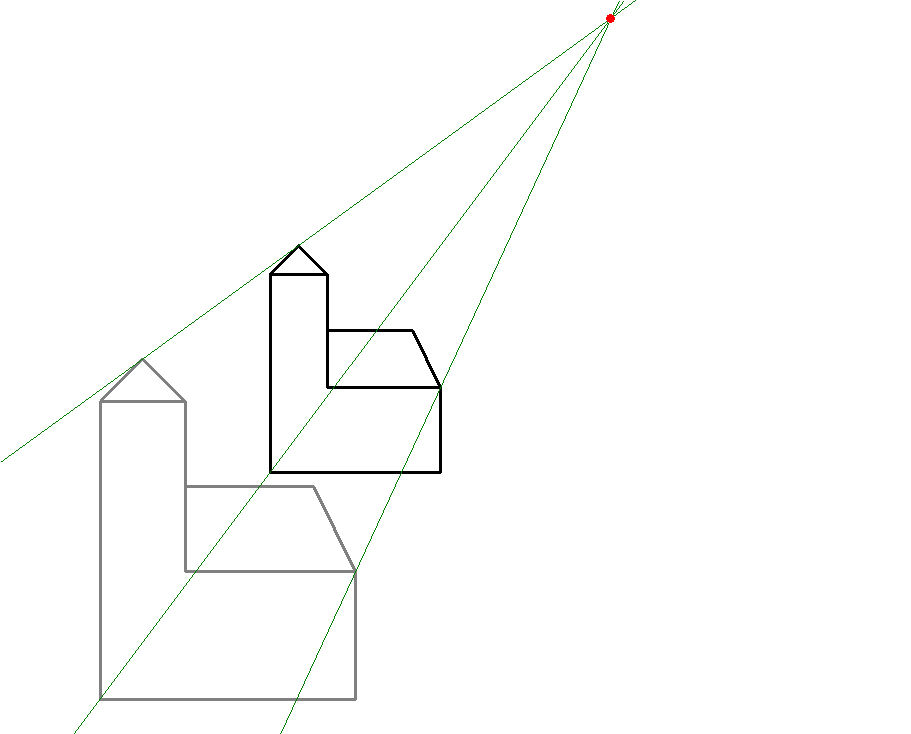
In Bild 10.1a sind beide Achsenaffinitäten ausführlich samt Achsen (Fixpunktgeraden) und Affinitätsstrahlen (Fixgeraden) dargestellt. Deutlich ist die Rehenfolge S->S_a->S_b der Einzelabbildungen zu erkennen. In Bild 10.1b sind nur noch die Affinitätsstrahlen der Kirchturmspitze und der gegenüberliegenden Kirchenecke sichtbar, alle anderen sind zur besseren Übersicht ausgeblendet; dafür ist dort auch die vertausche Verkettung aktiviert worden; somit entsteht die graue Kirche durch die Abbildungsreihenfolge S->S_a->S_ab und die orangefarbene Kirche durch die Abbildungs­reihenfolge S->S_b->S_ba. Das liefert die Erkenntnis, dass Vertauschen der Reihenfolge bei Verkettung von Abbildungen i.d.R. unterschiedliche Ergebnisse liefert (Mathematiker sagen die Verkettung ist i.a. nicht kommutativ).

Bild 10.1a - 10.1d

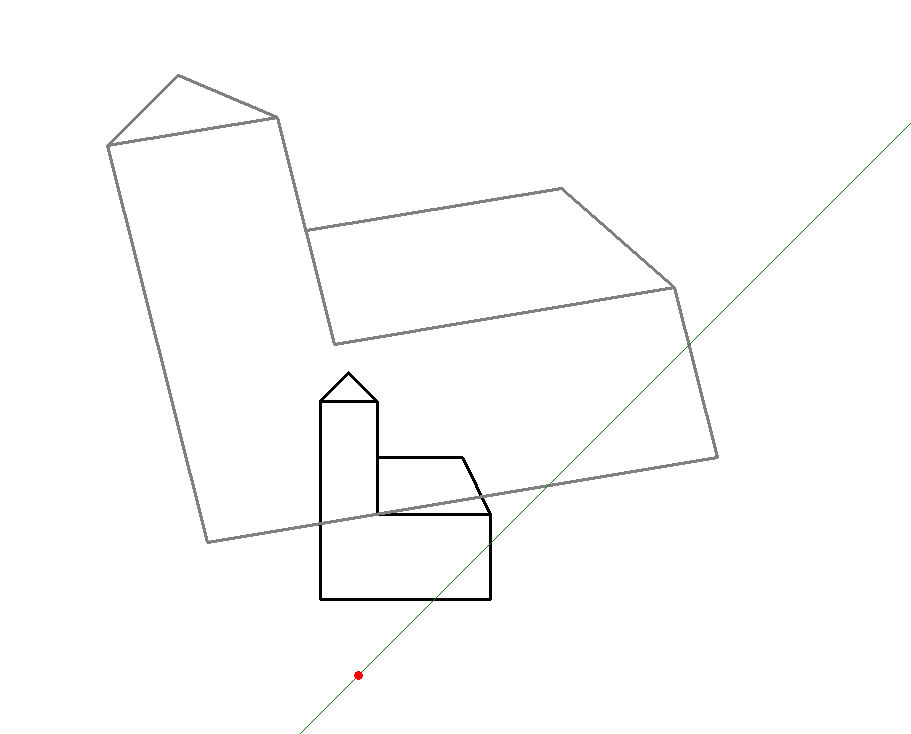
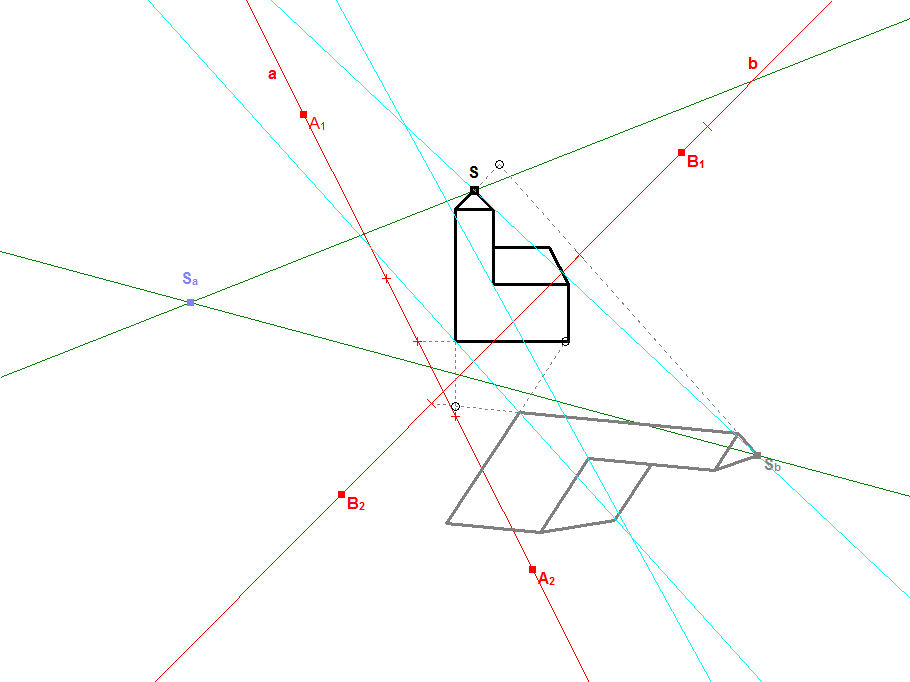
In den beiden Bildern 10.1c und 10.1d wird (wie in 10.1a) wieder nur eine Verkettung S->S_a->S_b dargestellt. In Bild 10.1c wird die Bedeutung der Achsen durch jeweils drei Geradenpaare (Urgerade-Bildgerade) hervorgehoben. In Bild 10.1d ist das blaue "Zwischenbild" ausgeblendet, dafür sind drei einander zugeordnete Geradenpaare helltürkisfarben eingezeichnet und es ergibt sich die Frage nach dem Abbildungstyp schwarz->grau.

Euler-Affinität

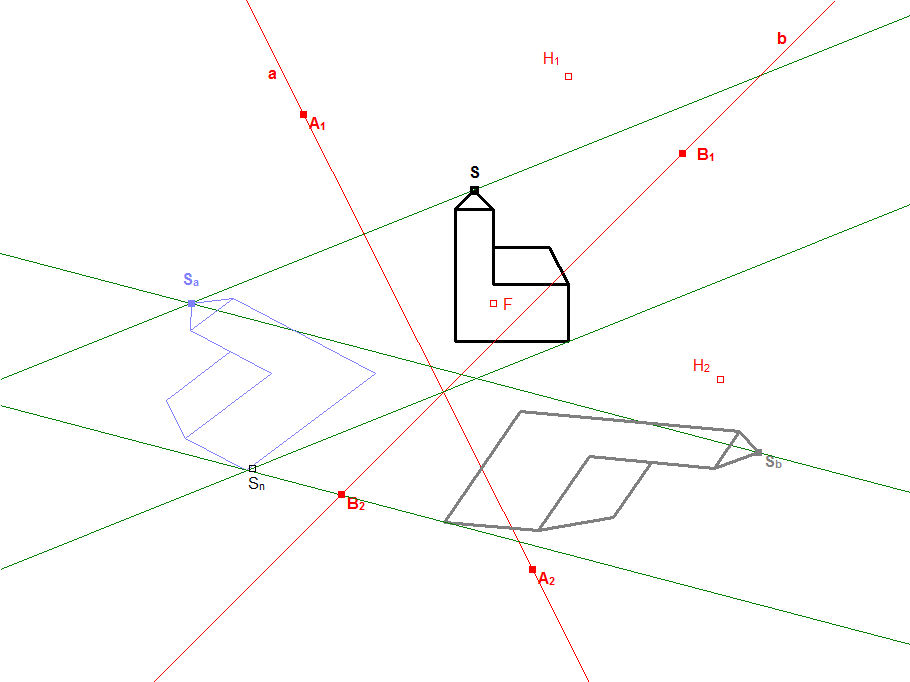
Im Folgenden wollen wir die Euler-Affinitäten weiter untersuchen, von denen wir inzwischen wissen, dass sie als Verkettung zweier Achsenaffinitäten darstellbar sind, wenn deren Affinitätsstrahlen wechelweise parallel zur jeweils anderen Achse sind. Dabei kommt es nicht auf die Reihenfolge der Abbildungen an. Man kann sich leicht davon überzeugen, dass die ursprünglichen Achsen zu (den einzigen) Fixgeraden "degradiert" werden und der Achsenschnittpunkt als einziger Fixpunkt erhalten bleibt.

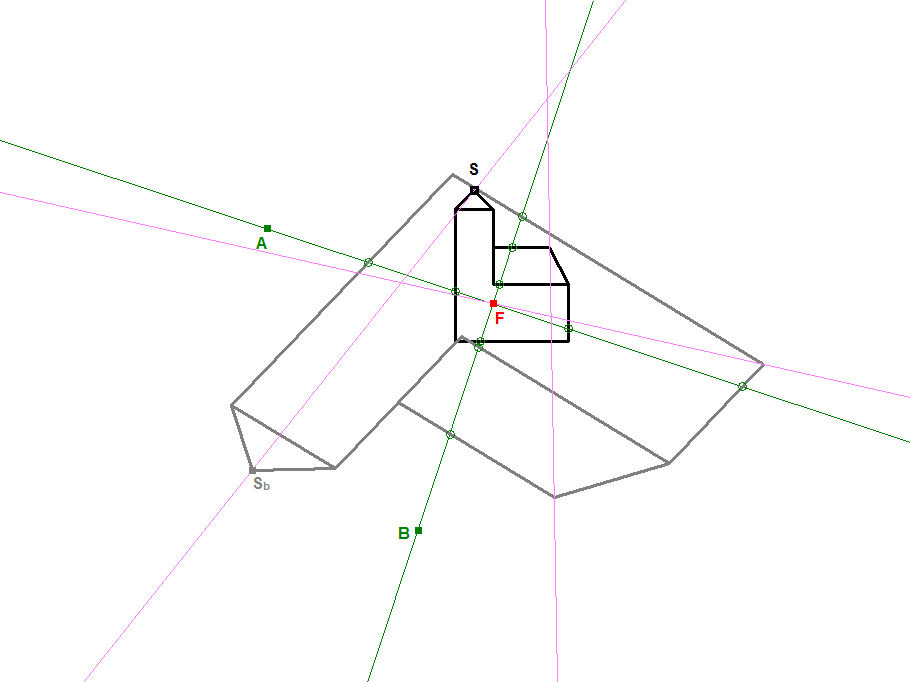
In den Bildern 10.2 ist nochmals die erste Euler-Affinität aus Abschnitt 7 dargestellt (Bild 7.2a), diesmal aber ohne den Umweg über Verkettungen; für DynaGeo genügte die Angabe der beiden Fixgeraden und des Bildes S der Kirchturmspitze, damit konnte DynaGeo die Abbildungsgleichung berechnen und die Kirche abbilden. Die Fixgeraden schneiden sich im (einzigen) Fixpunkt F.

Bild 10.2a - 10.2d

Um die Eigenschaft der Fixgeraden zu verdeutlichen, sind in Bild 10.2a deren Schnittpunkte mit den Kirchenkanten grün eingekringelt. Drei Hilfsgeraden sind pinkfarben eingezeichnet, die erste verbindet die beiden Kirchturmspitzen, die zweite die rechte obere Dachecke mit deren Bildpunkt, die dritte geht schräg durch den Fixpunkt. So ist zu erkennen, dass genau die Bilder aller grünen Schnittpunkte einer Fixgeraden mit den Kirchenkanten wieder auf dieser Fixgeraden landen. Für die drei pinkfarbenen Geraden gilt das nicht; diese haben (zunächst) keine erkennbare Funktion.

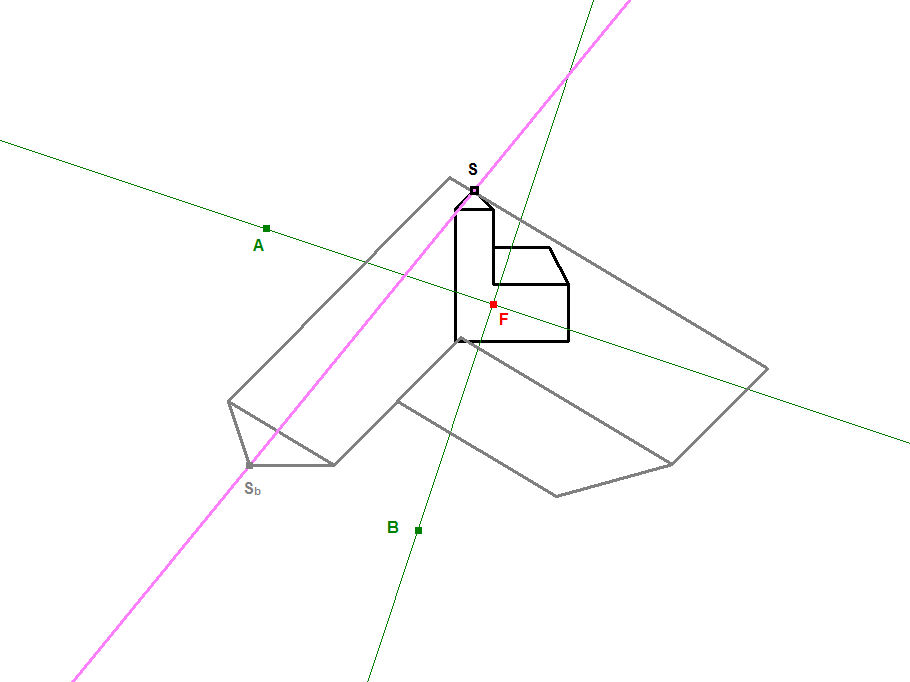
In Bild 10.2b ist die Verbindungsgerade der beiden Kirchturmspitzen, die zunächst keine Bedeutung hat, pinkfarben eingezeichnet. Aber was gechieht, wenn wir S so bewegen, dass diese Verbindungsgerade durch den Fixpunkt F geht?

In Bild 10.2c wird nochmals gezeigt, dass es nicht auf die Reihenfolge der beiden geeigneten Achsenaffintäten ankommt. Wenn man genau hinsieht, erkennt man, wie die graue Kirche deckungsgleich zur orangefarbenen ist (Bild vergrößern!).

Bild 10.2d bietet die Möglichkeit, die beiden Achsenaffintäten so zu manipulieren, dass eine beliebige Euleraffinität (oder die von Bild 7.2a) resultiert.

11. Systematik affiner Abbildungen der Euklidischen Ebene

Abschnitt überspringen

Für die systematische Untersuchung der affinen Abbildungen sind folgende Begriffe nötig: Vektorräume, Unter­vektorräume, lineare Abbildungen, Matrizen (Matrixschreibweise, Determinante), Eigenräume (Eigenvektoren, Eigen­werte, charakreristische Gleichung), Verkettung von Abbildungen. Erstaunlicherweise war das am Gymnasium in BW in Leistungskursen der Achziger-Jahre in ca. sieben Unterrichtswochen vermittelbar! Der Stoff um diese Begriffe gewährt Einblicke in grundlegende Sichtweisen der Mathematik, die in vielen anderen math.nat. Disziplinen Anwendung finden. Die folgenden drei DIN-A4-Seiten liefern eine (äußerst) knappe Zusammenfassung der dazu nötigen Theorie.

Bild 11.1a - 11.1c

Im Wahlfach Darstellende Geometrie werden u.a. Achsenaffinitäten behandelt. Diese runden den Stoff des Leistungskurses ab und sorgen für die nötige Anschaung, die in den sieben Leistungskurswochen nicht sehr vertieft werden konnte.

12. Quellenangaben

damals

Schulbücher/Lehrerfortbildung

Schaal-Glässner: Lineare Algebra und Analytische Geometrie; Didaktische Materialien für Grund- und Leistungskurse; Lehrerausbildung/Lehrerfortbildung; Klett 1983

Lambacher-Schweitzer: Themenhefte Mathematik; Lineare Algebra und Analytische Geometrie 2; Klett 1979

Jehle-Spremann-Zeidler: Lineare Geometrie in Leistungskursen; BSV 1977

Faber-Brixius: Lineare Algebra und Analytische Geometrie; Vektorräume und affine Geometrie; Klett 1974

^*) Ulshöfer-Tilp: Darstellende Geometrie in systematischen Beispielen; Arbeitsblätter;
(Mathematische Texte; Manz 1985) C.C. Buchner 2010

^*) Ulshöfer-Tilp: Darstellende Geometrie in systematischen Beispielen; Lehrerband;
(Mathematische Texte; Manz 1980) C.C. Buchner 2013 (Multimedia)

Faber: Geometrie 1 (Kongruenzabbildungen); Klett 1974

Faber: Geometrie 2 (Ähnlichkeitsabbildungen und Trigonometrie); Klett 1975

Andelfinger-Oettinger: Geometrie 1 und 2; Herder 1974

und heute

Programme zur dynamischen Geometrie/Mathematik

Wikipedia

Einzeldarstellunngen

affine Abbildungen
http://e-collection.library.ethz.ch/eserv/eth:25629/eth-25629-02.pdf Hans Walser
http://kilchb.de/faqmath5.html Joachim Mohr
http://m.schuelerlexikon.de/ma_abi2011/Affine_Abbildungen.htm Duden schuelerlexikon.de
http://www.cornelsen.de/sites/medienelemente_cms/mel_xslt_gen/progs/medien/mels_stat/mel_152016.pdf
    Cornelsen Verlag
http://www.mathematik.tu-dortmund.de/~algebra/DiskrGeom_2011-12/Materialien_DG/angeo_kap5.pdf
    Rudolf Scharlau
http://www.mspengler.de/BAUSTELLE/pdf2HP/AffinSkript.pdf Mario Spengler
http://www.ruhri.net/pdf/unterrichtsmaterial/Kurs_Matrizen_Aff_abb.pdf Alexander Ruhri
http://www.uni-regensburg.de/Fakultaeten/nat_Fak_I/Mat4/waldi/skriptlinalg/kapV_para3.pdf Walter Gubler
http://www2.klett.de/sixcms/media.php/229/Abbildungen%20und%20Matrizen.612823.pdf Ernst Klett Verlag

lineare Algebra/lineare Abbildungen/analytische Geometrie
http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXLA2.pdf Wolfgang Soergel
http://www.mathematik.uni-wuerzburg.de/~mutzb/angeo.pdf Otto Mutzbauer
http://www.mathematik.net/lin-abb/pdf-blumberg/LinA.pdf Sven Blumberg
http://www.staff.uni-oldenburg.de/wiland.schmale/Modul_Geometrie_WiSe_2010_2011/Kapitel_II_Par_6.pdf
    Wiland Schmale
http://www.staff.uni-oldenburg.de/wiland.schmale/Modul_Geometrie_WiSe_2010_2011/Kurzskript_gesamt_3.pdf
    Wiland Schmale
http://www.uni-math.gwdg.de/skripten/Aglaskript/agla.pdf Ina Kersten

Darstellende Geometrie
http://fma2.math.uni-magdeburg.de/~eid/Skript_DG_09-10.pdf Wolfram Eid
http://ebene11.com/darstellende-geometrie.html Fa. ebene elf
http://geometrie.eduhi.at/data/AK/grundkursdg05.pdf Helmut Pottmann
http://geometrie.uibk.ac.at/obsolete/Lehre/Vorkurs/ Hans-Peter Schröcker
http://name.umdl.umich.edu/ABN3249.0001.001 Darstellende Geometrie, von Gaspard Monge (1798)
http://servix.mathematik.uni-stuttgart.de/~stroppel/DarstGeo/ Markus Stroppel
http://vielemeyer.userweb.mwn.de/SkriptDGSS12.pdf Thomas Pöschl, Karin Vielemeyer
http://www.iaa.tu-bs.de/ws0708/dag/dag_2007.pdf Rainer Löwen
http://www.igpm.rwth-aachen.de/puetz/pub/igpm203.pdf Claus Pütz
http://www.mathematik.tu-darmstadt.de/Math-Net/Lehrveranstaltungen/Lehrmaterial/SS2005/DarGeoII/skript1-78.pdf
    Erich Hartmann
http://www.mathematik.tu-darmstadt.de/~ehartmann/cdg-skript-1998.pdf Erich Hartmann
http://www.uni-stuttgart.de/idg/pdf/vorlesungen/skript_1.pdf Wolfgang Knoll

diverses
http://ladamer.org/Feut/pdf/Kursbegleitung/dbv_vl/dbv_vl_kapitel3.pdf
    Uni Trier: Digitale Bildverarbeitung: Geometrische Entzerrung
http://public.beuth-hochschule.de/~pries/Vorlesungen/CAD1/TransformationenUndAbbildungen.pdf
http://wikis.zum.de/geometrie/index.php/Eigentlich_ganz_einfach_und_doch_so_kompliziert:_Punkte,_Geraden,_Ebenen
http://www.friedhelm-kuerpig.de/impressum.html Friedhelm Kürpig: geometrische Formen und Strukturen
http://www.geogebra.org/publications/diplomarbeit_geogebra.pdf Markus Hohenwarter
http://www.iazd.uni-hannover.de/~erne/lina2/dateien/linAlg7.pdf Marcel Erné: Quadriken
http://www.mfo.de/math-in-public/education/teachers-training/fortbildung_2.pdf Oliver Labs: Theorie und
    Visualisierung von algebraischen Kurven und Flächen
http://www.stauff.de/matgesch/dateien/abbildungsmatrizen.htm Heiner Stauff

zur Startseite

Dietrich Tilp  |  02.2014 | 11.2022