Zentralprojektion / Perspektive |
| Stand: 13.01.2017 |
0. Vorbemerkungen
 Abschnitt überspringen
Abschnitt überspringen
 Dieser Text bietet eine Einführung in die Zentralprojektion unter historischem Bezug auf die Renaissance. Dazu werden wir anhand von Dürers Kupferstich Der heilige Hieronymus im Gehäus (s.r.) die Gesetze der Zentralprojektion aufspüren. Mit Hilfe des Programms EUKLID DynaGeo von Roland Mechling können Sie den Kenntnisstand Dürers selbst nachvollziehen. Dazu wird in diesem Text der
Dieser Text bietet eine Einführung in die Zentralprojektion unter historischem Bezug auf die Renaissance. Dazu werden wir anhand von Dürers Kupferstich Der heilige Hieronymus im Gehäus (s.r.) die Gesetze der Zentralprojektion aufspüren. Mit Hilfe des Programms EUKLID DynaGeo von Roland Mechling können Sie den Kenntnisstand Dürers selbst nachvollziehen. Dazu wird in diesem Text der ![]() DynaGeoJ-Viewer von R. Mechling verwendet. Alle Konstruktionen sind im Haupttext nur verkleinert dargestellt. Durch Anklicken gelangen Sie zu den zugehörigen DynaGeo-Fenstern in sinnvoller Größe.
DynaGeoJ-Viewer von R. Mechling verwendet. Alle Konstruktionen sind im Haupttext nur verkleinert dargestellt. Durch Anklicken gelangen Sie zu den zugehörigen DynaGeo-Fenstern in sinnvoller Größe.
Aktueller Hinweis:
Wenn Sie in diesen DynaGeo-Fenstern keine dynamischen Inhalte sehen, müssen Sie den IE als Browser verwenden, s. ![]() Tipps zur Installation. Und wenn im IE in den DynaGeo-Fenstern die Zeichnungen beim Scrollen nicht richtig mitlaufen, dann müssen Sie in deren Kontextmenü (Rechtsklick!) die Zeichnung neu laden.
Tipps zur Installation. Und wenn im IE in den DynaGeo-Fenstern die Zeichnungen beim Scrollen nicht richtig mitlaufen, dann müssen Sie in deren Kontextmenü (Rechtsklick!) die Zeichnung neu laden.
Während die Zentralprojektion (dieser Text) eher in den "Bildenden Künsten" zu finden ist, wird die Parallelprojektion (Text ![]() Affine Geometrie / Affinitäten) eher in "technischen Dokumentationen" eingesetzt .
Affine Geometrie / Affinitäten) eher in "technischen Dokumentationen" eingesetzt .
Die Idee zu diesem Skript geht auf Klaus Ulshöfer zurück, der 1980 die treibende Kraft unseres Arbeitsbuches Darstellende Geometrie in systematischen Beispielen war. Dr. Ulshöfer hat schon immer von Dürers Heiligem Hieronymus als Vorlage für den Unterricht in Darstellender Geometrie an Gymnasien in Baden-Württemberg geschwärmt. Daher hat er in den Achtzigern mehrere Aufsätze zum Thema veröffentlicht und später anlässlich einer Neuauflage unseres Arbeitsbuches den Heiligen Hieronymus gleich am Anfang des Buches als Einführung in die Ziele der DG einfügen lassen. Seine Aufsätze behandeln Dürers Hieronymus klassisch, d.h. mit dem Reißzeug. Im vorliegenden Skript liegt der Schwerpunkt dagegen auf dem dynamischen Entdecken der Gesetzmäßigkeiten mittels DynaGeo.
Vor gut dreissig Jahren (d.h. im Zeitalter der Umdruckmatritzen) musste Dr. Ulshöfer im Fachhandel erst hochwertige Exemplare von Dürers Stich besorgen und dann mit dem "Reißzeug" experimentieren. Für jeden Versuch war eine neue Kopie fällig.
Heutzutage dagegen lädt man sich einfach ein hochaufgelöstes Bild von Dürers Stich aus Wikipedia herunter, bindet es als Hintergrundbild in einem Programm wie DynaGeo ein und schon kann man im Bild konstruieren (bei Misslingen ggf. beliebig oft wiederholbar), d.h. Punkte und Linien setzen und ggf. auf Knopfdruck wieder löschen oder genauer/anders positionieren usw.. Zum exakten Konstruieren lässt sich das Bild samt Zeichnung beliebig vergrößern und hinterher wieder verkleinern.
Albrecht Dürer war wohl einer der ersten Künstler im deutschen Sprachraum, der seine Erkenntnisse und Erforschungen in anschaulichen Lehrbüchern ("Büchlein") veröffentlichte; siehe ![]() Quellen/Linkliste. In der Linkliste sind ferner zwei sehr lesenswerte Seiten aufgeführt: Georg Wick mit über 1200 Perspektive-Bildern von der Antike bis 2015 und Martin Mißfeldt mit einem Aufsatz über die kunsthistorische Entwicklung der Perspektive.
Quellen/Linkliste. In der Linkliste sind ferner zwei sehr lesenswerte Seiten aufgeführt: Georg Wick mit über 1200 Perspektive-Bildern von der Antike bis 2015 und Martin Mißfeldt mit einem Aufsatz über die kunsthistorische Entwicklung der Perspektive.

1. Einführung
 Abschnitt überspringen
Abschnitt überspringen
Gaspard Monge (1746-1818) gilt allgemein als der Begründer der mathematisch basierten Darstellenden Geometrie. Aber natürlich gab es lange vor ihm bereits ernsthafte Auseinandersetzungen mit dem Wesen der Abbildung realer Szenarien.
So ist Albrecht Dürer (1471-1528) wohl einer der ersten Bildenden Künstler, welcher der Abbildungslehre (ca. 250 Jahre früher!) mathematisch auf den Grund ging und seine Erkenntnisse in Buchform veröffentlichte.
Dem Wikipedia-Hauptartikel über Dürer ist folgender Absatz entnommen:
... Wissenschaftshistorisch bemerkenswert jedoch ist seine Underweysung der messung mit dem zirckel und richtscheyt in Linien ebnen unnd gantzen corporen, das erste Mathematikbuch deutscher Sprache mit bedeutenden neuen Erkenntnissen. Im Titel ist das Wort „Messung” im Zusammenhang mit der damals vorherrschenden Übersetzung „Messkunst” für das griechische Wort Geometrie zu verstehen und bedeutet im heutigen Wortsinn eher „Konstruktion”. In der Underweysung definiert Dürer spezielle Kurven, insbesondere erstmalig die Muschellinie und die Pascalsche Schnecke (die er selber wegen ihrer Konstruktionsvorschrift „Spinnenlinie” nannte), gibt eine neue Konstruktion einer Ellipse an, erkennt Ellipse, Parabel und Hyperbel als Kegelschnitte (und ist damit Vorläufer von Gaspard Monge), zeigt ein neuartiges und sehr genaues Verfahren zur Winkeldreiteilung und stellt die Tangens-Funktion grafisch dar (motiviert durch das ganz praktische Problem, die Schrifthöhe in Abhängigkeit von der Höhe ihrer Anbringung so zu staffeln, dass alle Zeilen gleich hoch erscheinen). ...
 Dürer hat die Underweysung 1525 aufgeteilt in vier "Büchlein" veröffentlicht. Die folgenden beiden Stiche aus dem vierten "Büchlein" zeigen, wie praktisch Dürer bei der Erforschung der Zentralperspektive vorgegangen ist, wie er den einäugigen Sehprozess experimentell nachempfunden hat (Perspektive = Hindurchsehung). Den Heiligen Hieronymus hat er bereits 1514 veröffentlicht, also über zehn Jahre vor Erscheinen des vierten "Büchleins".
Dürer hat die Underweysung 1525 aufgeteilt in vier "Büchlein" veröffentlicht. Die folgenden beiden Stiche aus dem vierten "Büchlein" zeigen, wie praktisch Dürer bei der Erforschung der Zentralperspektive vorgegangen ist, wie er den einäugigen Sehprozess experimentell nachempfunden hat (Perspektive = Hindurchsehung). Den Heiligen Hieronymus hat er bereits 1514 veröffentlicht, also über zehn Jahre vor Erscheinen des vierten "Büchleins".
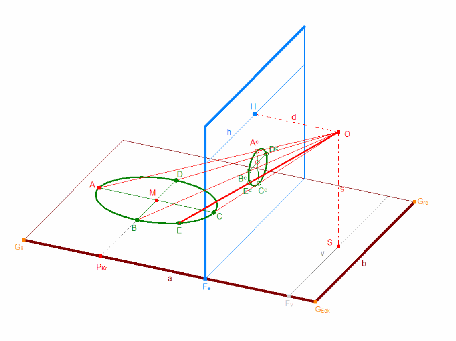 In den Stichen oben sind die Begriffe Grundebene, Bildebene, Auge, Durchstoßpunkte und Sehstrahlen materiell nachempfindbar ("gegenständliche" Kunst). Im rechten Stich wird das Bild der Laute im ursprünglichen Sinn konstruiert.
In den Stichen oben sind die Begriffe Grundebene, Bildebene, Auge, Durchstoßpunkte und Sehstrahlen materiell nachempfindbar ("gegenständliche" Kunst). Im rechten Stich wird das Bild der Laute im ursprünglichen Sinn konstruiert.
Dabei hat Dürer den Vorgang des Zentralpojizierens als zentralprojiziertes Bildnis dargestellt, wie z.B. an den Fenstersimsen ablesbar ist.
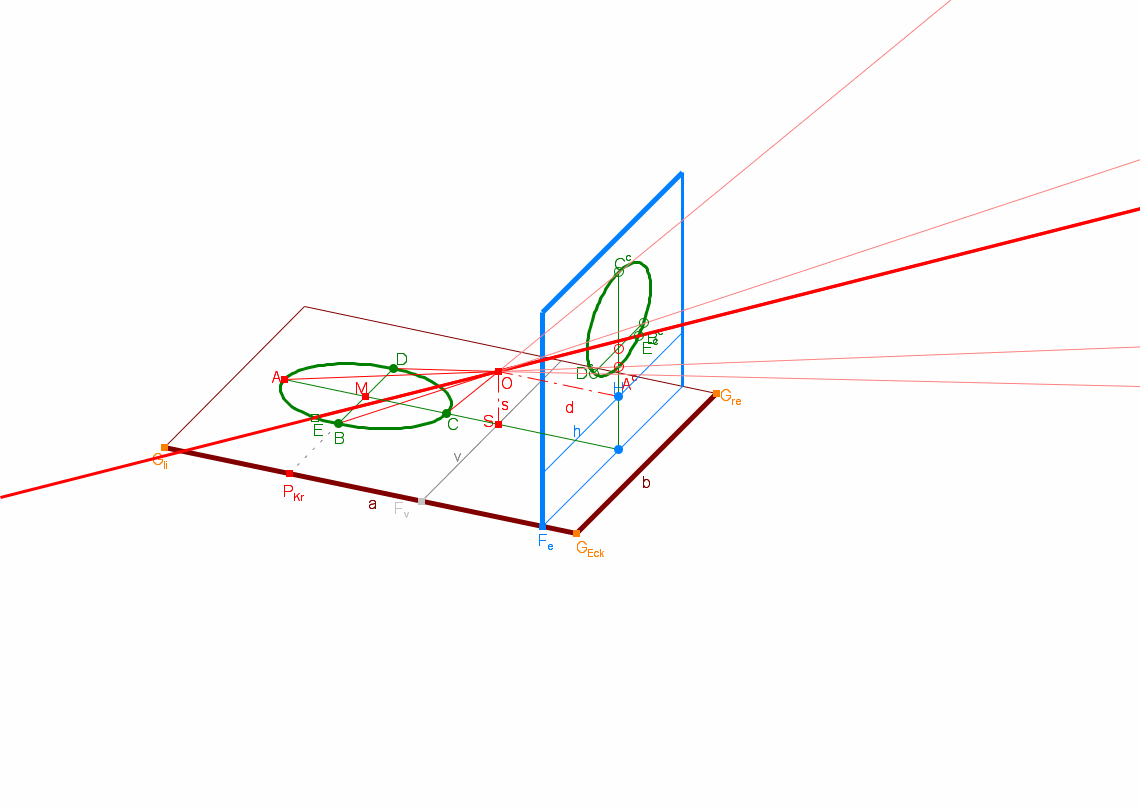
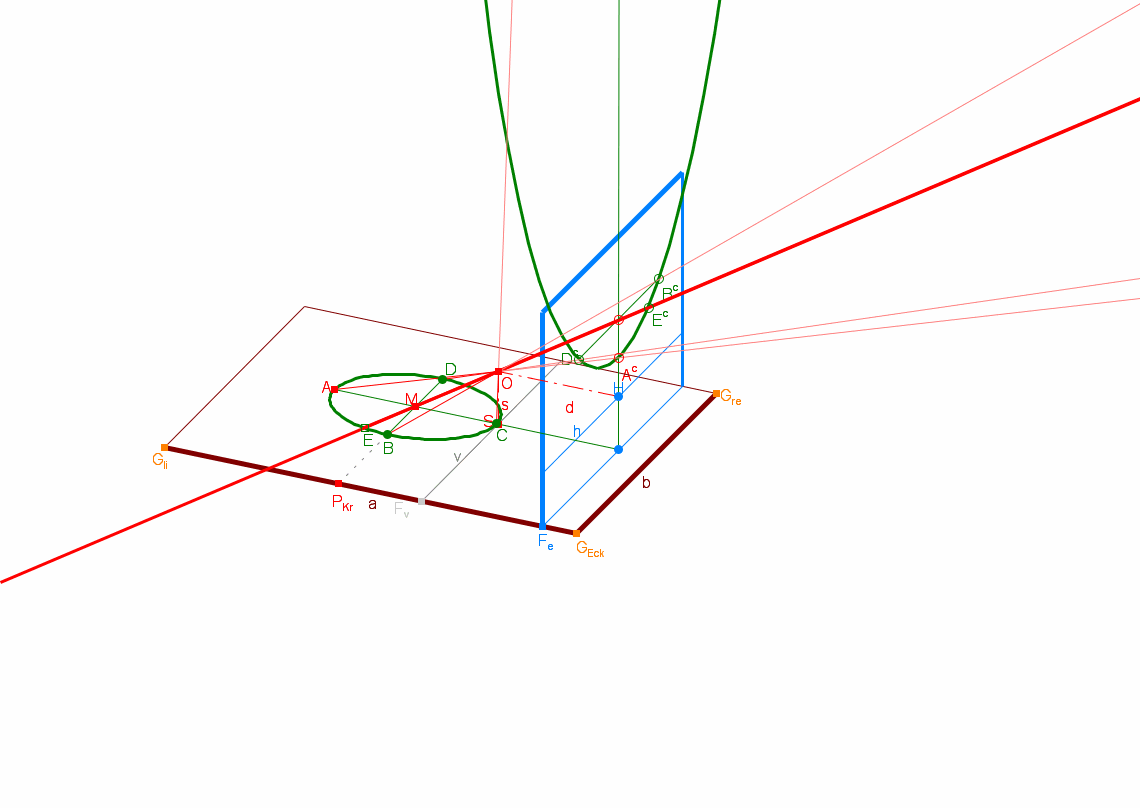
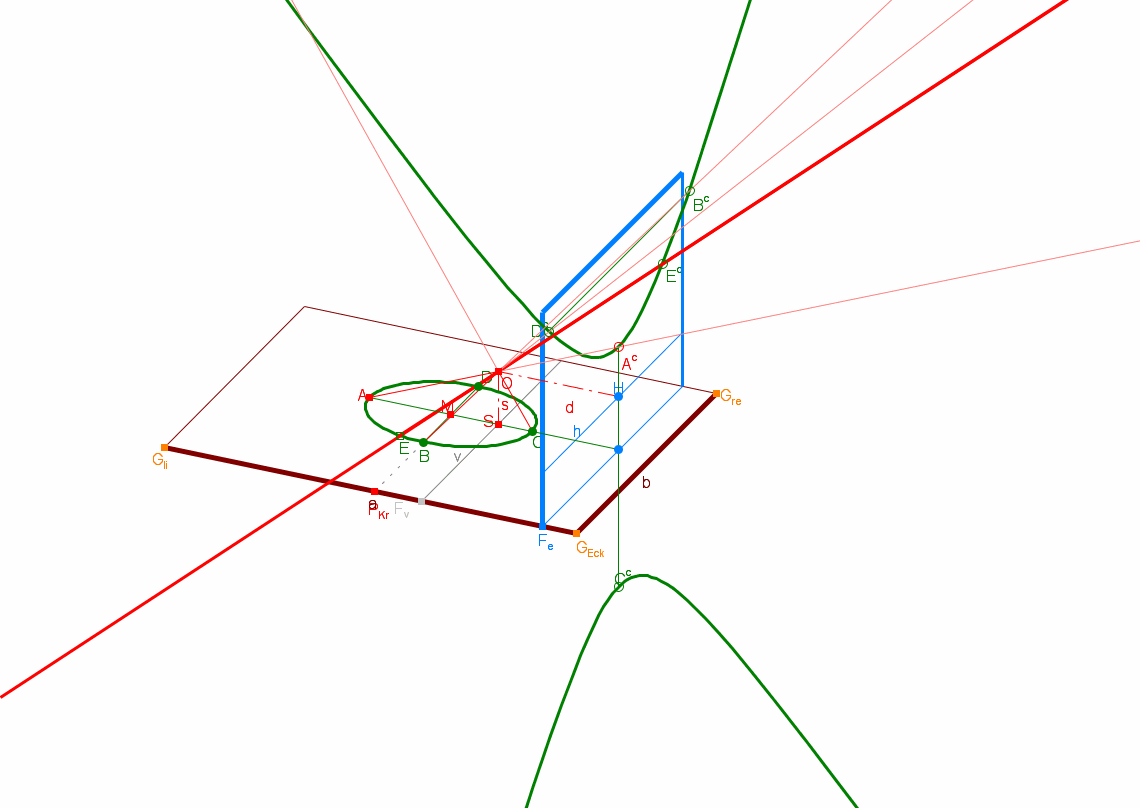
Dürers Laute oben entspricht der Ellipse im DynaGeo-Bild darunter. Wenn Sie das Bild anklicken, gelangen Sie zum DynaGeo-Fenster, in dem Sie die Anordnung variieren können, indem Sie die Lage der Grundebene ändern und die Ellipse und die Bildebene verschieben. Bereits dabei können Sie einige Gesetzmäßigkeiten beobachten. Und Sie werden dabei ausser der Ellipse auch die anderen Kegelschnitte Parabel und Hyperbel kennenlernen (s.u.).
Dabei stellen wir den Vorgang des Zentralpojizierens als parallelprojiziertes Bild dar!

2. Der heilige Hieronymus
 Abschnitt überspringen
Abschnitt überspringen
Sophronius Eusebius Hieronymus (347 - 420) war Kirchenvater, Heiliger, Gelehrter und Theologe der alten Kirche. Er gehört in der katholischen Kirche zusammen mit Ambrosius von Mailand, Augustinus und Papst Gregor I. zu den vier spätantiken Kirchenlehrern des Abendlandes (wikipedia).
Wir wollen in diesem Abschnitt vor allem scharf beobachtend zusammenstellen, welche Erkenntnisse Dürer über die Zentralprojektion im Stich verarbeitet hat. Im nächsten Abschnitt lassen wir die Theorie folgen.
 Wie ist das Zimmer ausgerichtet?
Wie ist das Zimmer ausgerichtet?
Stellen Sie sich einen Schuhkarton ohne Deckel vor, den Sie "in Augenhöhe" in ein Regal stellen, so dass die Öffnung auf Sie zu zeigt. In den Schuhkarton ist ein Modell des Zimmers eingebaut. Steht der Karton quer zu Ihnen oder schräg?
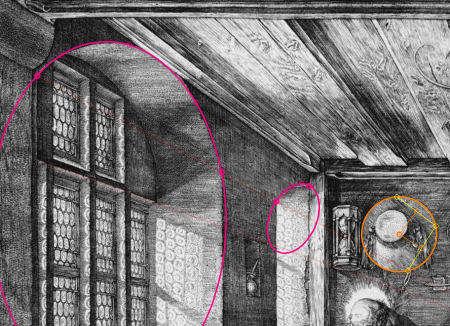
Wenn wir die "Vertikale" in der Fensterwand aufnehmen und die Horizontale in Decke und Fußboden ergänzen, dann verlaufen diese in guter Näherung lotrecht zueinander (s.r., grüne Linien). Wenn das Zimmer rechtwinkelig gebaut ist, dann ist die Rückwand parallel zur Bildebene ausgerichtet. Die Regale an der Rückwand verlaufen ebenfalls waagrecht, bestätigen also die Vermutung, genauso wie die kreisrunde Hutkrempe.
Die Vertikalen und die Horizontalen verlaufen in unterschiedlicher Raumtiefe, sind also windschief zueinander; trotzdem können wir sagen, dass sie lotrecht zueinander sind.
Auch die vorderseitige und die rückseitige Kante des Arbeitstisches verlaufen waagrecht; also ist der Tisch parallel zur Rückwand ausgerichtet. Die Sitzbank dagegen nicht, sie steht schräg neben dem Tisch.
 Im Stich sind die herausragenden Richtungen die Vertikale, die Horizontale und die "Tiefenlinien", die sich in einem Punkt schneiden, dem Fluchtpunkt (s.l.; hellblaue Linien). Dieser Punkt heißt Hauptpunkt H. Der Hauptpunkt ist also der Fluchtpunkt der Tiefenlinien.
Im Stich sind die herausragenden Richtungen die Vertikale, die Horizontale und die "Tiefenlinien", die sich in einem Punkt schneiden, dem Fluchtpunkt (s.l.; hellblaue Linien). Dieser Punkt heißt Hauptpunkt H. Der Hauptpunkt ist also der Fluchtpunkt der Tiefenlinien.
Die Tischplatte wirkt sehr tief; ist der Tisch quadratisch? Wie schräg steht die Bank neben dem Tisch?
 Diese Fragen hängen eng zusammen. Wenn wir annehmen, dass Dürer stolz war auf sein math. Wissen über die Abbildungslehre, dann ist kein Teil des Arrangements zufällig. Also wird die Tischplatte vermutlich horizontal im Raum stehen und quadratisch sein mit der Folge, dass deren Diagonalen einander rechtwinklig schneiden und horizontal unter 45° zur Rückwand verlaufen müssen. Und die Sitzbank mit recheckiger horizontaler Sitzplatte und horizontaler Lehne wird vermutlich schräg unter genau 45° zur Rückwand stehen. Lassen sich die Vermutungen anhand des Stichs beweisen?
Diese Fragen hängen eng zusammen. Wenn wir annehmen, dass Dürer stolz war auf sein math. Wissen über die Abbildungslehre, dann ist kein Teil des Arrangements zufällig. Also wird die Tischplatte vermutlich horizontal im Raum stehen und quadratisch sein mit der Folge, dass deren Diagonalen einander rechtwinklig schneiden und horizontal unter 45° zur Rückwand verlaufen müssen. Und die Sitzbank mit recheckiger horizontaler Sitzplatte und horizontaler Lehne wird vermutlich schräg unter genau 45° zur Rückwand stehen. Lassen sich die Vermutungen anhand des Stichs beweisen?
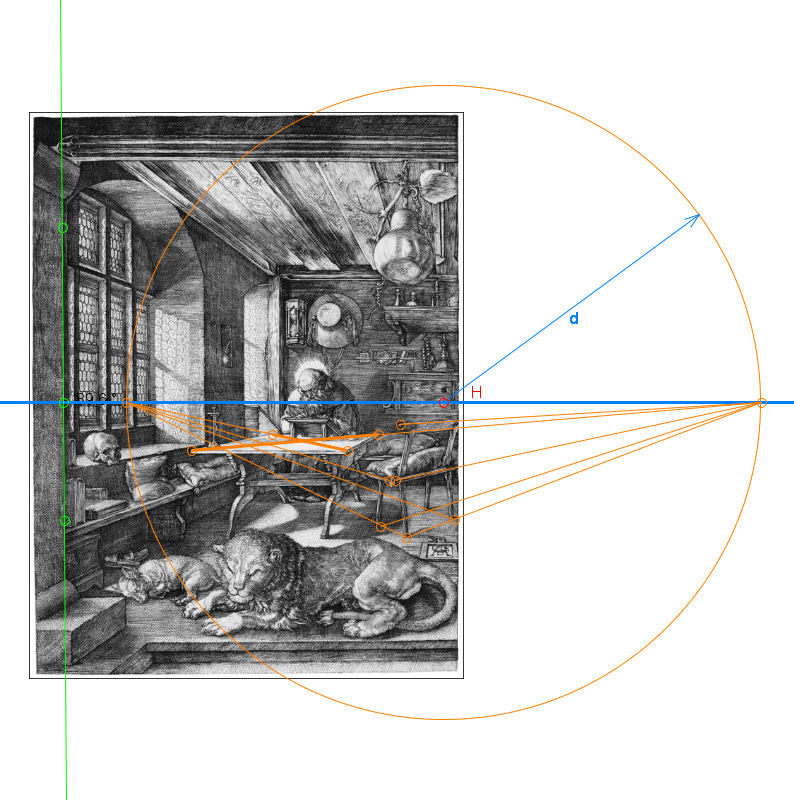
Alle zueinander parallelen Geraden haben einen gemeinsamen Fluchtpunkt, wie wir im Stich exemplarisch anhand der hellblauen Tiefenlinien sehen konnten. Alle zueinander parallelen horizontalen Linien (s.r., orange Linien) haben diesen Fluchtpunkt auf dem Horizont, das ist eine Horizontale durch den Hauptpunkt (blaue Linie), wie im nächsten Abschnitt gezeigt wird.
Nun gibt es im Stich etliche horizontale Geraden, die nach rechts hinten verlaufen (vermutlich unter 45° und daher parallel). Diese müssen also einen gemeinsamen Fluchtpunkt rechts auf dem Horizont besitzen, was sich im Stich verfizieren lässt. Und es gibt im Stich einige horizontale Geraden, die nach links hinten verlaufen (vermutlich unter 45° und daher parallel). Deren Fluchtpunkt muss also links auf dem Horizont liegen, was sich ebenfalls im Stich ergibt.
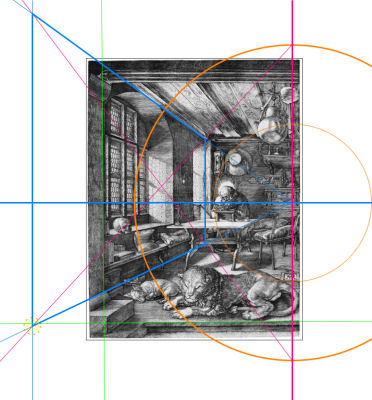 Dass die Tischdiagonalen senkrecht zueinander sind, ist bisher nur eine Vermutung (quadratischer Tisch), aber dass die von den Sitzbankbeinen gebildete Grundfläche ein Rechteck bildet, dürfen wir fordern. Dieses Rechteck ist im Stich nicht sehr präzise bestimmbar, weil die Sitzbankbeine dick sind, aber unsere Vermutungen über die 45°-Linien helfen beim Positionieren. Wir finden so im Stich also zwei klare Fluchtpunkte auf dem Horizont. Und dann zeigt sich überraschenderweise, dass diese beiden Fluchtpunkte vom Hauptpunkt gleich weit entfernt sind. Diese Entfernung werden wir Distanz d nennen. Sie gibt auch den Abstand des Auges O von der Bildebene an (also die Distanz von Dürers Auge zur Bildebene). Das alles beweist unsere 45°-Vermutung, wie im nächsten Abschnitt gezeigt wird. Im Bild ist der Distanzkreis eingezeichnet (Kreis um H mit Radius d); er entspricht einem 90°-Sehkegel. Zusätzlich ist dünn ein Kreis um H mit Radius d/2 eingezeichnet, was einem 53°-Sehkegel entspricht.
Dass die Tischdiagonalen senkrecht zueinander sind, ist bisher nur eine Vermutung (quadratischer Tisch), aber dass die von den Sitzbankbeinen gebildete Grundfläche ein Rechteck bildet, dürfen wir fordern. Dieses Rechteck ist im Stich nicht sehr präzise bestimmbar, weil die Sitzbankbeine dick sind, aber unsere Vermutungen über die 45°-Linien helfen beim Positionieren. Wir finden so im Stich also zwei klare Fluchtpunkte auf dem Horizont. Und dann zeigt sich überraschenderweise, dass diese beiden Fluchtpunkte vom Hauptpunkt gleich weit entfernt sind. Diese Entfernung werden wir Distanz d nennen. Sie gibt auch den Abstand des Auges O von der Bildebene an (also die Distanz von Dürers Auge zur Bildebene). Das alles beweist unsere 45°-Vermutung, wie im nächsten Abschnitt gezeigt wird. Im Bild ist der Distanzkreis eingezeichnet (Kreis um H mit Radius d); er entspricht einem 90°-Sehkegel. Zusätzlich ist dünn ein Kreis um H mit Radius d/2 eingezeichnet, was einem 53°-Sehkegel entspricht.
Im nebenstehenden Bild wurde versucht nachzuweisen, dass die linke Seitenwand ebefalls quadratisch sein könnte. Dazu muss deren linke Begrenzung konstruiert werden, da sie hinter der Säule am linken Stichrand verschwindet. Obwohl die so gefundene untere Wandecke gut mit der waagrechten Treppenkante im Vordergrund fluchtet, passt das Ergebnis nicht recht zur Gestaltung der linken Zimmerwand.
Die Anordnung des Raumes mit einer Vertikalen und einer Horizontalen und auf einen Fluchtpunkt zulaufenden Tiefenlinien, wie sie im Hieronymus zu sehen ist, setzt Dürer praktisch in allen Stichen und Holzschnitten ein, die architektonischen Bezug haben. Diese Darstellungsmethode heißt Ein-Fluchtpunkt-Perspektive oder kürzer Zentralperspektive oder auch Frontalperspektive.
Später werden wir noch die Zwei-Fluchtpunkt-Perspektive oder (Über-)Eck-Perspektive und die Drei-Fluchtpunkt-Perspektive kennenlernen. Manche Autoren verwenden Zentralperspektive als Überbegriff für Ein-, Zwei- und Drei-Fluchtpunkt-Perspektiven, andere sehen in der Zentralperspektive im engeren Sinn die Ein-Fluchtpunkt-Perspektive.
In der darstellenden/konstruktiven Geometrie geht es um Anschaulichkeit und Maßhaltigkeit. Der Techniker braucht maßhaltige Zeichnungen (z.B. Grundriß und Aufriß), um ein Objekt exakt nachbauen zu können. Leider steht die Maßhaltigkeit in Konkurrenz zur Anschaulichkeit. Je anschaulicher ein Objekt dargestellt werden soll, desto "perspektivischer" muss dies geschehen. Dabei versteht man unter Perspektive alle Abbildungsverfahren, die unter Inkaufnahme von Verzerrungen, den Raum anschaulich linear (also dem menschlichen Sehen nachempfunden) abbilden. Die perspektiven Affinitäten sind Parallelprojektionen, die Zentralperspektive ist eine Zentralprojektion. Eine Fischaugenkamera dagegen erzeugt nichtlineare Bilder.

3. Fern- und Fluchtpunkte, Zentralperspektive
 Abschnitt überspringen
Abschnitt überspringen
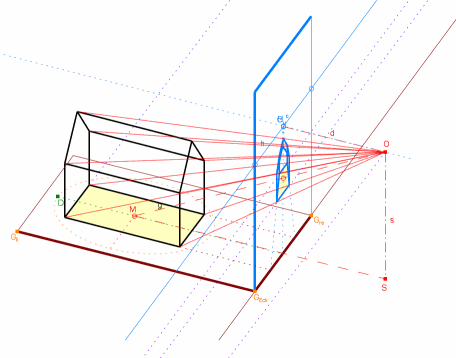 In den folgenden Bildern untersuchen wir anhand eines Hauses in Zentralpespektive die Grundlagen der Zentralprojektion. D.h. wir werden Fernpunkte von Geraden und deren Bilder, die Fluchtpunkte, betrachten. Über die Bilder gelangen Sie zur zugehörigen dynamischen DynaGeo-Seite.
In den folgenden Bildern untersuchen wir anhand eines Hauses in Zentralpespektive die Grundlagen der Zentralprojektion. D.h. wir werden Fernpunkte von Geraden und deren Bilder, die Fluchtpunkte, betrachten. Über die Bilder gelangen Sie zur zugehörigen dynamischen DynaGeo-Seite.
Rechts stehen die Längskanten der Grundfläche des Hauses senkrecht zur Bildebene; damit stehen die Giebelfronten des Hauses parallel zur Bildebene (Frontalperspektive / Zentralperspektive). Die Längskantengeraden durchstoßen die Bildebene in den Spurpunkten G1 und G2. Die Bilder der Längskantengeraden gehen durch diese Spurpunkte und gemeinsam durch den Hauptpunkt H (Begründung s. Fenster 3). Damit ergeben sich die Bilder der Längskanten über die zugehörigen Sehstrahlen im Schnitt mit den Längskantengeraden.
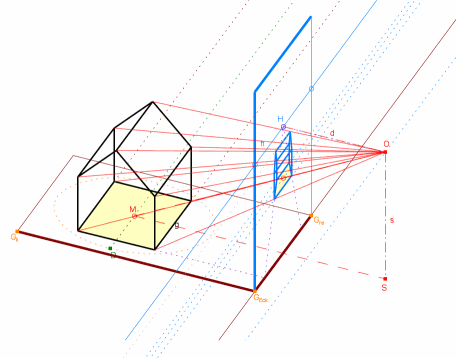 Links ist das Haus um 90° gedreht. Nun stehen die Querkanten der Grundfläche senkrecht zur Bildebene und damit die Längsfrontern parallel zur Bildebene. Die Querkantengeraden haben die Spurpunkte G3 und G4. Damit gehen die Bilder der Querkantengeraden durch diese Spurpunkte und gemeinsam durch den Hauptpunkt.
Links ist das Haus um 90° gedreht. Nun stehen die Querkanten der Grundfläche senkrecht zur Bildebene und damit die Längsfrontern parallel zur Bildebene. Die Querkantengeraden haben die Spurpunkte G3 und G4. Damit gehen die Bilder der Querkantengeraden durch diese Spurpunkte und gemeinsam durch den Hauptpunkt.
So hat es bereits Dürer dargestellt. Im folgenden Bild erkennen wir, warum das so sein muss. Dort betrachten wir nur die beiden Geraden g und g1 der einen Längsfront. Deren Spurpunkte in der Bildebene sind G und G1.
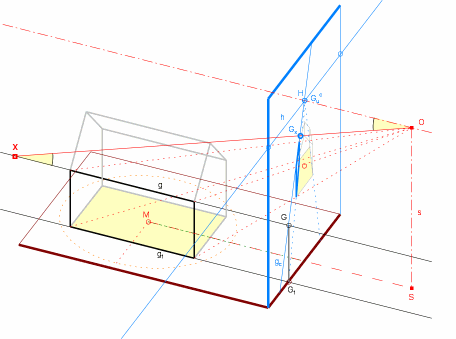 Das Lot vom Auge O auf die Bildebene mit dem Lotfußpunkt H ist parallel zu g und g1, da alle drei senkrecht zur Bildebene stehen.
Das Lot vom Auge O auf die Bildebene mit dem Lotfußpunkt H ist parallel zu g und g1, da alle drei senkrecht zur Bildebene stehen.
Auf g ist links der Hilfspunkt X samt Sehstrahl von O aus eingezeichnet. Wenn Sie X längs g wandern lassen, dann wandert dessen Bildpunkt Gx als Durchstoßpunkt des Sehstrahls mit der Bildebene irgendwo in der Bildebene und beschreibt dabei die Bildgerde gc.
Die Lotgerade OH, die Gerade g und der Sehstrahl von X bilden eine Wechselwinkelfigur, liegen also in einer gemeinsamen Ebene, der Sehstrahlebene der Gerden g. Zwei (nichtparallele) Ebenen schneiden sich immer in einer Geraden. Also schneiden sich die Sehstrahlebene und die Bildebene in einer Geraden; also ist die Zentralprojektion geradentreu.
Allgemein gilt: Jede Gerade g durchstößt die Bildebene im Spurpunkt G (oder ist parallel zur Bildebene). Also ist G zugleich ein Punkt Gc der Bildgeraden gc. Um die Bildgerade gc zeichnen zu können, wird ein zweiter Punkt benötigt. Den erhält man, indem man den gedanklichen Hilfspunkt X auf der Geraden g von der Bildebene wegwandern lässt und dabei beobachtet, wohin sich dessen Sehstrahl bewegt. Je ferner X wegwandert, desto spitzer wird der Winkel zwischen g und dem Sehstrahl. Wenn F unendlich fern ist (X heißt dann Fernpunkt Gu von g), ist dieser Winkel auf Null geschrumpft, der Sehstrahl ist also parallel zur Geraden. Der Durchstoßpunkt dieses Sehstrahls ist der Fluchtpunkt Guc der Geraden g (Guc ist das Bild von Gu) und dieser Fluchtpunkt ist der gesuchte zweite Punkt zur Bestimmung von gc.
Verläuft die Gerade g horizontal, dann auch der Sehstrahl zu deren Fernpunkt; dann liegt ihr Fluchtpunkt Guc auf dem Horizont h. Verläuft die Gerade in der Grundebene, liegt zusätzlich ihr Spurpunkt G = Gc auf der Grundspur e. Beides ist in Fenster 3 der Fall.
Alle zur Bildebene senkrechte Geraden, wie z.B. g1, haben die selbe Richtung, also den selben Fernpunkt, also den gleichen Sehhstrahl zum Fernpunkt und somit den gleichen Fluchtpunkt, nämlich den Hauptpunkt H. Wird ein Bild so erstellt, dass wichtige Linien ihren Fluchtpunkt im Hauptpunkt haben, spricht man von Zentralperspektive.
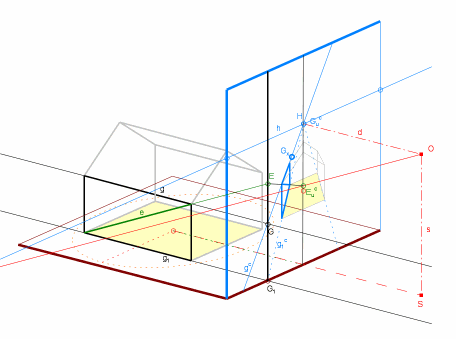
Im nebenstehenden Bild untersuchen wir eine Diagonale e der Längsfront. Die ganze Längsfront hat die Spur f in der Bildebene, also hat die Gerade e dort den Spurpunkt E; der Fluchtpunkt ist Euc. Also geht das Bild ec von e durch E und Euc, wobei Euc auf der Fluchtspur (Vertikale durch H) der Längsfront liegt.
Auch in zentralperspektiven Bildern gibt es natürlich Geraden, die nicht senrecht zur Bildebene stehen. Ein Beispiel ist die Sitzbank in Dürers Hieronymus. Im folgenden Bild untersuchen wir mit Hilfe der Grundfläche der Sitzbank (rechtwinklig angenommen) die innere Orientierung der Aufnahmesituation im Hieronymus-Stich.
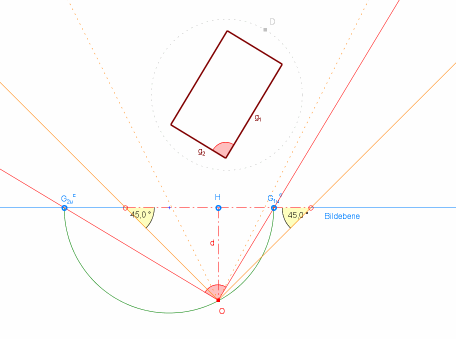
Die Szene ist von oben gesehen; die Grundfläche der Sitzbank erscheint somit als unverzerrtes Rechteck und die Bildebene davor "projizierend" als Gerade. Zu den zwei Kanten g1 und g2 gehören die beiden Flucktpunkte G1uc und G2uc in der Bildebene. Weil vom Auge O aus G1uc und G2uc wegen der rechtwinkligen Sitzbank ebenfalls unter einem rechten Winkel erscheinen, bilden G1uc, O und G2uc ein rechtwinkliges Dreieck, um das der zugehörige Thaleskreis gezeichnet werden kann. Die Höhe d im Dreieck ist die gesuchte Distanz des (Dürerschen) Auges zur Bildebene.
Wenn das Rechteck in 45°-Lage steht, fällt das Thaleskreisdreieck mit dem vorgegebenen rechtwinklig-gleichschenkligen Dreieck zusammen (ausprobieren!), dessen Basis den Durchmesser des Distanzkreises darstellt. Somit ist klar, dass die Fluchtpunkte aller 45°-Geraden auf dem Distanzkreis liegen müssen und weil das Drehen des Rechtecks nichts an der inneren Orientierung ändert, ist mit Hilfe der Fluchtpunkte zweier sich schneidender rechtwinkliger Geraden die Distanz festgelegt.
Wenn man das Auge O parallel zur Bildebene bewegt, ändert sich die innere Orientierung (die Distanz) nicht. Die Zeichnung rund um O wird einfach quer verschoben. Bewegungen auf die Bildebene zu oder weg von ihr ändern jedoch die Größe dieses Teils der Zeichnung und somit auch die Distanz (die innere Orientierung).
Aber bei jeder Bewegung ändert sich die gegenseitige Lage von O zum Objekt (Sitzbank), was sich auf die Zeichung auswirken wird. D.h., die äußere Orintierung der Anordnung ändert sich. Machen Sie sich klar, dass sich die innere Orientierung nicht ändert, wenn die Bank verschoben wird; aber deren Bild wird sich ändern. Daher unterscheiden wir innere und äußere Orientierung bei der Beschreibung von Abbildungssituationen. Im Bild entspricht die äußere Orientierung nicht derjenigen im Hieronymus, schon deshalb nicht, weil das Auge beweglich ist (ausprobieren!).

4. Dürers Zentralperspektive und Kreisabbildung
 Abschnitt überspringen
Abschnitt überspringen


 Nebenstehend sind zwei weitere Beispiele Dürers Zentralperspektive dargestellt. Die Holzschnitte stammen aus dem Zyklus "Marienleben": Mariä Verkündigung (1503) weist 17 Kreisbögen parallel zur Bildebene auf, in Vermählung Marias mit Joseph (1504) ist eine kleine Kuppel enthalten (
Nebenstehend sind zwei weitere Beispiele Dürers Zentralperspektive dargestellt. Die Holzschnitte stammen aus dem Zyklus "Marienleben": Mariä Verkündigung (1503) weist 17 Kreisbögen parallel zur Bildebene auf, in Vermählung Marias mit Joseph (1504) ist eine kleine Kuppel enthalten (![]() http:// schlesischesammlungen.eu).
http:// schlesischesammlungen.eu).
Das Bild rechts aussen, Presentazione della Vergine al Tempio (ca. 1467), stammt von Fra Carnevale (alias Bartolomeo Corradini; 1420 - 1484; ![]() http://www. mfa.org/collections/object/presentation-of-the-virgin-in-the-temple-32587). Auch er nützt intensiv die Zentralperspektive, um Kreisbögen rationell abbilden zu können. Er wagt sich aber auch an nach hinten verlaufende Kreisbögen. Schließlich wurde die Zentralperspektive in Italien entwickelt.
http://www. mfa.org/collections/object/presentation-of-the-virgin-in-the-temple-32587). Auch er nützt intensiv die Zentralperspektive, um Kreisbögen rationell abbilden zu können. Er wagt sich aber auch an nach hinten verlaufende Kreisbögen. Schließlich wurde die Zentralperspektive in Italien entwickelt.
Auch Dürer zeichnete nach hinten verlaufende Kreisbögen, aber sehr zurückhaltend. Dabei hatte er bereits in seinem ersten "Büchlein" Ellipse, Parabel und Hyperbel als Kegelschnitte beschrieben. Da der Fensterbogen des hinteren Fensters sehr kurz ist, kann nichs schlüssig gezeigt werden, ob der zugehörige Ellipsenbogen "richtig" konstruiert ist.
Da die Zentralprojektion nicht teilverhältnistreu ist, werden insbesondere Mitten nicht auf Mitten abgebildet, mit der Folge, dass Kreismittelpunke nicht auf die Mittelpunkte der zugehörigen Bildellipsen abgebildet werden. Daher ist die Ellipsenabbildung bei Zentralprojektion sehr kompliziert.
Wie weiter oberen bereits ausgeführt ist, heißt die Darstellungstechnik Zentralperspektive / Frontalperspektive. Ihr Wesen ist die Verwendung des einen Fluchtpunkts (im Hauptpunkt), daher könnte sie auch als Ein-Fluchtpunkt-Perspektive charakterisiert werden. In der Renaissance (15.-16. Jahrhundert) sind derartige Dastellungen sehr üblich.
Es fällt aber auf , dass das "Zentrum" der Zentralprojektion, der Hauptpunkt, meist gar nicht in Bildmitte liegt, sondern an den rechten oder linken Rand des "Bildfensters" gerückt wird. Diese Asymmetrie steigert die Wirkung der Darstellung. So z.B. kommt die Säulenflucht im Bild von Fra Carnevale erst richtig zur Geltung.
Aber in den praktischen Übungen in Abschnitt 3 kann das Haus so gedreht werden, dass keine Front mehr parallel zu Bildebene steht. Dann entsteht eine Übereck-Perspektive (s. nächsten Abschnitt).

5. Übereck-Perspektive und Drei-Fluchtpunkt-Perspektive
 Abschnitt überspringen
Abschnitt überspringen
 Obwohl Dürer die Zentralperspektive favorisiert, ist ihm die Übereck-Perspektive sehr wohl bekannt. So steht die Sitzbank sogar in spezieller Übereck-Perspektive innerhalb des zentralpespektivischen Bildes vom heiligen Hieronymus. Und auch diese Sitzbank ist richtig "konstruiert", wie in Abschnitt 2 gezeigt wird. Dort ist auch zu erkennen, dass bei der Übereck-Perspektive zwei Fluchtpunkte auftreten müssen, daher auch der Name Zwei-Fluchtpunkt-Perspektive.
Obwohl Dürer die Zentralperspektive favorisiert, ist ihm die Übereck-Perspektive sehr wohl bekannt. So steht die Sitzbank sogar in spezieller Übereck-Perspektive innerhalb des zentralpespektivischen Bildes vom heiligen Hieronymus. Und auch diese Sitzbank ist richtig "konstruiert", wie in Abschnitt 2 gezeigt wird. Dort ist auch zu erkennen, dass bei der Übereck-Perspektive zwei Fluchtpunkte auftreten müssen, daher auch der Name Zwei-Fluchtpunkt-Perspektive.
Details in Übereck-Perspektive, wie die Sitzbank, kommen in vielen Bildern Dürers vor. In seiner Zeichnung Aachener Rathaus von 1520/21 liegt zwar (wieder) Zentralperspektive vor, aber das "Detail" übernimmt hier die Hauptrolle: der Hauptbaukörper steht hier nicht frontal, sondern schief (s.r., Kontrast nachgearbeitet).
Die folgenden beiden Fotos zeigen Zwei-Fluchtpunkt-Perspektive (s.l.u) und Drei-Fluchtpunkt-Perspetive (s.r.u.) eines modernen Gebäudes. Das rechte Bild entstand als typische "Knipserei": Damit die ganze Höhe abgebildet werden konnte, musste die Kamera etwas nach oben gekippt werden, wodurch die typischen stürzenden Linien entstanden (besonders auffällig am rechten Rand) Das linke Bild entstand aus dem rechten durch "Entzerrung" mit einem Bildbearbeitungprogramm.

6. Längen und Winkelmessung
 Abschnitt überspringen
Abschnitt überspringen

7. Quellen / Linkliste
https://de.wikipedia.org/wiki/Albrecht_Dürerhttp://de.wikipedia.org/wiki/Der_heilige_Hieronymus_im_Gehäus
http://de.wikipedia.org/wiki/Hieronymus_(Kirchenvater)
http://commons.wikimedia.org/wiki/Category:Underweysung_der_Messung
"Underweysung der messung mit dem zirckel un[d] richtscheyt, in Linien ebnen unnd gantzen corporen"
Originale der vier "Buechlein"
http://de.wikisource.org/wiki/.../Erstes_Buch Der aller scharff sinnigst Euclides / hat den Grund ...
http://de.wikisource.org/wiki/.../Zweites_Buch Hernach folget das ander buechlein von den ebnen felderen
http://de.wikisource.org/wiki/.../Drittes_Buch Das dryt buechlein / von den Corperlichen dingen
http://de.wikisource.org/wiki/.../Viertes_Buch Das Viert buechlein
http://digital.slub-dresden.de/werkansicht/dlf/12477/1/
"Opera Alberti Dureri, Das ist, Alle Bücher des weitberühmbten und Künstreichen Mathematici und Mahlers
Albrechten Durers von Nürenberg"
http://www.schlesischesammlungen.eu/Kunstobjekte/Grafik/Duerer-Albrecht-Vermaehlung-Marias-mit-Joseph
http://www.aendres.de/Texte/Duerer_Geometrie_6.pdf
http://www.mathe.tu-freiberg.de/~hebisch/cafe/duerer.html
http://de.wikipedia.org/wiki/Perspektive
http://unterricht.kunstbrowser.de/downloads/perspektivelinearperspektivmodell.pdf
http://zeichnen.gemutlichkeit.de/html/Zeichnen_Grundlagen/Perspektive/index.php
http://stubber.math-inf.uni-greifswald.de/mathematik+kunst/hilfsmittel.html
http://www.gwick.ch/Perspe/PerspeHome.html Georg Wick: Perspektive in Bildern
[in der Bildenden Kunst von den Anfängen bis zur Gegenwart]:
http://www.gwick.ch/Perspe/Pictures/Zeit137.html –450 bis 1379
http://www.gwick.ch/Perspe/Pictures/Zeit143.html 1380 bis 1436
http://www.gwick.ch/Perspe/Pictures/Zeit145.html 1437 bis 1455
http://www.gwick.ch/Perspe/Pictures/Zeit146.html 1456 bis 1468
http://www.gwick.ch/Perspe/Pictures/Zeit148.html 1469 bis 1486
http://www.gwick.ch/Perspe/Pictures/Zeit150.html 1487 bis 1507
http://www.gwick.ch/Perspe/Pictures/Zeit153.html 1508 bis 1537
http://www.gwick.ch/Perspe/Pictures/Zeit158.html 1538 bis 1585
http://www.gwick.ch/Perspe/Pictures/Zeit164.html 1592 bis 1648
http://www.gwick.ch/Perspe/Pictures/Zeit167.html 1649 bis 1677
http://www.gwick.ch/Perspe/Pictures/Zeit177.html 1685 bis 1770
http://www.gwick.ch/Perspe/Pictures/Zeit188.html 1771 bis 1884
http://www.gwick.ch/Perspe/Pictures/Zeit194.html 1885 bis 1940
http://www.gwick.ch/Perspe/Pictures/Zeit198.html 1941 bis 1989
http://www.gwick.ch/Perspe/Pictures/Zeit200.html 1990 bis 2015
http://www.martin-missfeldt.de/ Kunst, Malerei und Gemälde von Martin Mißfeldt
http://www.martin-missfeldt.de/perspektive-zeichnen-tutorial/
Perspektive [1]: perspektivisch zeichnen mit Fluchtpunkt und Fluchtlinien
http://www.martin-missfeldt.de/perspektive-zeichnen-tutorial/perspektive-albrecht-duerer.php
Perspektive [2]: Analyse des Dürer Holzschnitts "Der Zeichner der Laute"
http://www.martin-missfeldt.de/perspektive-zeichnen-tutorial/perspektive-kunst-entwicklung.php
Perspektive [3]: Kunsthistorische Entwicklung der Perspektive
http://it.wikipedia.org/wiki/Fra_Carnevale
http://www.unterricht.kunstbrowser.de/downloads/perspektivelinear2fluchtpunktperspektive.pdf
Die Übereckperspektive mit zwei Fluchtpunkten
http://blog.skd.museum/wp-content/uploads/2012/08/perspektive-pdf1.pdf Perspektivische Darstellung in der Renaissance
http://www.uni-stuttgart.de/iek/all/download/skripte/gruda/13_FrontalPerspektive.pdf Frontalperspektive / Über-Eck-Perspektive
http://www.thiele-architekt.de/pdf/Raumsprache-A5.pdf Handbuch zur Architekturskizze
http://www.mathematik.uni-muenchen.de/~pareigis/Papers/Perspektive.pdf
http://www.lehrerfreund.de/technik/1s/perspektive-kurs-1/4258
http://www.lehrerfreund.de/technik/1s/perspektive-kurs-2/4259
http://www.lehrerfreund.de/technik/1s/perspektive-kurs-3/4260
http://www.lehrerfreund.de/technik/1s/perspektive-kurs-4/4261
http://www.lehrerfreund.de/technik/1s/perspektive-kurs-5-zwei-fluchtpunkte/4361
http://name.umdl.umich.edu/ABN3249.0001.001 Darstellende Geometrie, von Gaspard Monge (1798)

Dietrich Tilp | 06.01.2017